Publicado originalmente en MagazineZX número 10 (noviembre 2004)
El juego de la vida de John Conway
Hasta el momento hemos aprendido a instalar y compilar programas con z88dk, utilizando para ellos ejemplos prácticos basados en la creación de una Aventura Conversacional de Texto. En nuestros anteriores números, y gracias a los ejemplos de aventuras conversacionales, hemos descubierto cómo z88dk nos permite utilizar las diferentes funciones estándar de ANSI C para realizar nuestros pequeños programas.
El Juego de la Vida
Esta entrega del curso de z88dk se basará en un ejemplo práctico completo comentado: la implementación para z88dk del clásico “Juego de la Vida” de John Conway. Conway fue un matemático de la Universidad de Cambridge que en 1970 inventó un sencillo juego no interactivo que permitía simular un entorno de vida basado en células individuales que morían o se reproducían mediante unas sencillas reglas.
La mejor definición del Juego de la Vida de John Conway la podemos encontrar en la Wikipedia:
El juego de la vida es un autómata celular diseñado por el matemático británico John Horton Conway en 1970. Es el mejor ejemplo de un autómata celular. Hizo su primera aparición pública en el número de octubre de 1970 de la revista Scientific American, en la columna de juegos matemáticos de Martin Gardner. Desde un punto de vista teórico, es interesante porque es equivalente a una máquina universal de Turing, es decir, todo lo que se puede computar algorítmicamente se puede computar en el juego de la vida.
Desde su publicación, ha atraído mucho interés debido a la gran variabilidad de la evolución de los patrones. La vida es un ejemplo de emergencia y autoorganización. Es interesante para los científicos, matemáticos, economistas y otros observar cómo patrones complejos pueden provenir de la implementación de reglas muy sencillas.
La vida tiene una variedad de patrones reconocidos que provienen de determinadas posiciones iniciales. Poco después de la publicación, se descubrieron el pentominó R y el planeador (en inglés glider), lo que atrajo un mayor interés hacia el juego. Contribuyó a su popularidad el hecho de que se publicó justo cuando se estaba lanzando al mercado una nueva generación de miniordenadores baratos, lo que significaba que se podía jugar durante horas en máquinas que, por otro lado, no se utilizarían por la noche. Para muchos aficionados, el juego de la vida sólo era un desafío de programación y una manera divertida de usar ciclos de la CPU. Para otros, sin embargo, el juego adquirió más connotaciones filosóficas. Desarrolló un seguimiento casi fanático a lo largo de los años 1970 hasta mediados de los 80.
Cabe decir que el “Juego de la Vida” causó furor en 1970, hasta el punto en que se convirtió en el divertimento de muchos “hackers programadores” la implementación del Juego de la Vida en los potentes mainframes de Universidades y Centros de Cálculo. Hoy en día sigue siendo un buen ejercicio de programación para aquellos que empiezan a dar clases de Informática, ya que la programación es muy sencilla y no requiere grandes conocimientos del lenguaje de programación utilizado.
Reglas básicas de El Juego de la Vida
El Juego de la Vida se basa en una matriz de un tamaño determinado (como por ejemplo, 50×50, ó 32×32), que podríamos considerar nuestro “caldo de cultivo”, en la cual mueren y se crean células. De forma efectiva, una célula es un 1 en una posición determinada de la cuadrícula mientras que un “espacio vacío” se representa mediante un cero.
El Juego de la Vida no requiere interacción por parte del usuario: a partir de un estado inicial (células diseminadas por el caldo de cultivo) se aplican una serie de reglas y se obtiene una nueva generación de células en dicho “caldo”. Esta nueva generación será la entrada para volver a aplicar las reglas, y así sucesivamente.
Las reglas para cada una de las “celdillas” de nuestro caldo de cultivo son:
- Si una celdilla está ocupada por una célula y tiene una sola célula vecina o ninguna (se consideran células vecina aquellas que están alrededor de ella, en cualquiera de las 8 casillas posibles que la rodean), esa célula muere por soledad.
- Si una celdilla está ocupada por una célula y tiene 4 o más células vecinas, muere por superpoblación.
- Si una celdilla está ocupada por una célula y tiene 2 ó 3 células vecinas, sobrevive a la siguiente generación.
- Si una celdilla está vacía (no está ocupada por una célula) y tiene 3 células vecinas, nace una nueva célula en su lugar para la siguiente generación.
Con estas sencillas reglas se obtienen unos resultados sorprendentes, ya que aparecen patrones de evolución que se cambian, realizan formas y caminos determinados, etc. Así, aparece el “planeador o caminador” (un conjunto de células que se desplazan), el “explosionador” (conjunto de células que parecen formar la onda expansiva de una explosión), etc.
Implementación del Juego de la Vida en el Spectrum
Antes de codificar propiamente en C lo que es el “juego”, veamos cómo sería el pseudocódigo que implementaría el diseño definido por Conway:
tablero[ANCHO][ALTO]
Programa Principal:
Crear_Generación_Aleatoria()
repetir:
Dibujar_Generación_Actual()
Calcular_Siguiente_Generación()
si se pulsa la tecla 'r':
Crear_Generación_Aleatoria()
fin repetir
El anterior sería el esqueleto de la función principal, que como podréis ver en el código, se corresponde con la siguiente función main():
//--- Funcion principal main() ---------------------------- int main( void ) { int i; GenLife(); while(1) { DrawLife(); Life(); if( getk() == 'r' ) GenLife(); } return(0); }
Con esto, el programa principal realizaría la impresión en pantalla de la generación actual de células (para que podamos ver la evolución visualmente) mediante la función Dibujar_Generación_Actual(). Tras esto, se calcularía la siguiente generación de células aplicando las reglas anteriormente explicadas, dentro de la función Calcular_Siguiente_Generacion() . Si en cualquier momento se pulsa la tecla 'r' (en nuestro programa) se modificará de nuevo el tablero aleatoriamente para añadir nuevas células y que en el siguiente paso del bucle comience de nuevo la simulación.
Crear_Gen_Aleatoria()
La función Crear_Generación_Aleatoria() se encargaría de vaciar el “tablero de juego” o “caldo de cultivo” (poner todos sus elementos a cero), y rellenar algunas celdillas aleatorias con células (valores 1). Dicha función la hemos definido en pseudocódigo de la siguiente forma:
Crear_Generacion_Aleatoria:
Para todo 'x' y todo 'y':
tablero[x][y] = 0
tablero_temporal[x][y] = 0
Repetir NUM_CELULA veces:
xcel = x_aleatoria()
ycel = y_aleatoria()
tablero_temporal[ xcel ][ ycel ] = 1
En nuestro pseudocódigo utilizamos una matriz [ancho*alto] para representar el caldo de cultivo. Dentro de esta matriz, cada posición matriz[x][y] puede contener o no una célula mediante los valores de 0 y 1 respectivamente. Así, en un tablero de 32×32, podemos poner una célula justo en la mitad del tablero ejecutando “matriz[16][16] = 1”.
dimensiones: ancho = 32
alto = 16
Tablero: mapa[ancho][alto]
Temporal: temp[ancho][alto]
Crear célula: mapa[x][y] = 1
Borrar célula: mapa[x][y] = 0
En el caso de z88dk, en lugar de utilizar matrices bidimensionales del tipo [ancho][alto] necesitaremos utilizar un vector de tamaño [ancho*alto], ya que la versión actual de z88dk no soporta el primer tipo de matrices.
De esta forma, ahora los accesos al mapa de células quedarían así:
Tablero: mapa[ancho*alto]
Temporal: temp[ancho*alto]
Crear célula: mapa[(y*ancho) + x] = 1
Borrar célula: mapa[(y*ancho) + x] = 0
Es decir, que un array unidimensional se puede tratar como un array bidimensional donde cada una de las líneas se coloca a continuación de la anterior, y acceder a cada uno de sus elementos mediante “posición = (y * ancho_fila) + x”.
Para facilitar el tratamiento de los datos, en el código definimos los siguientes macros o #defines (que hacen las veces de funciones, pero que en lugar de ser llamadas son “incluidas”, evitando un CALL con sus PUSHes, POPs y sus RETs):
#define Celula(x,y) (mapa[((y)*32)+(x)]) #define TempCelula(x,y) (temp[((y)*32)+(x)])
De esta forma en nuestro código podemos hacer simplemente:
valor = Celula( 10, 10 ); Celula( 11, 12 ) = 1;
Y al compilar, este código será sustituído por:
valor = (mapa[((10)*32)+(10)]); (mapa[((12)*32)+(11)]) = 1;
Obviamente el código utilizando nuestros #defines es mucho más claro y más fácil de mantener. Si encontramos una manera más óptima de acceder a las células, sólo hará falta modificarlo en el #define para que al recompilar, el cambio se aplique en todo el código fuente (en lugar de tener que ir cambiándolo llamada a llamada, como nos ocurriría en caso de no haber usado #defines). Y como ejemplo de “mejora” de nuestro define, vamos a acelerar la velocidad del cálculo de la posición del array cambiando la multiplicación por 32 por un desplazamiento de bits a la izquierda, ya que en un número almacenado de forma binaria, multiplicar por una potencia n-sima de 2 equivale a desplazar n veces a la izquierda el número que queríamos multiplicar. De esta, forma como 32 es 2 elevado a la quinta potencia, nos queda que:
x * 32 = x << 5
Reemplazando esto en nuestro #define:
#define Celula(x,y) (mapa[((y)<<5)+(x)]) #define TempCelula(x,y) (temp[((y)<<5)+(x)])
Se deja al lector como ejercicio realizar la prueba de reemplazar «5 por *32 en el código fuente y verificar que efectivamente, el desplazamiento de bits es mucho más rápido que la multiplicación (puede apreciarse visiblemente en la velocidad de la simulación).
El código final correspondiente para nuestra función de generación aleatoria de estados iniciales es el siguiente:
//--- Rellenar el tablero con valores aleat. -------------- void GenLife( void ) { int x, y, i; // Inicializar la semilla de numeros aleatorios srand(clock()); BORDER(0); CLS(0); printf( "\x1B[%u;%uH",(21),(1)); printf(" ZX-Life - MagazineZX - z88dk "); printf(" (r) = nueva generacion aleatoria "); // limpiamos el tablero de celulas for( i=0; i< NUM_CELULAS; i++) { x = (rand() % (ANCHO-2)) +1; y = (rand() % (ALTO-2)) +1; TempCelula(x,y) = Celula(x,y) = 1; } }
Como cosas que destacar de esta función tenemos:
- srand(clock()) : Inicializa la semilla de números aleatorios usando como base el reloj del Spectrum (por reloj del Spectrum consideramos el contador que tiene el sistema y que contabiliza el número de segundos transcurridos desde el inicio del ordenador). Esto asegura que cada vez que ejecutemos el programa (en un Spectrum real o un emulador que no tenga carga automática del .tap al abrirlo con él), tengamos una secuencia de números aleatorios diferentes y no obtengamos siempre la misma generación inicial de células. Los números aleatorios los obtendremos posteriormente con rand().
- BORDER() y CLS(): Estas 2 funciones cambian el color del borde y borran la pantalla respectivamente. Están implementadas en ensamblador, como puede verse en el código fuente de ZXlife . La primera cambia el borde mediante un OUT del valor del borde en el puerto que se utiliza para ello, mientras que la segunda utiliza LDIR para borrar la zona de pantalla de memoria. Este ejemplo nos permite ver lo sencillo que es integrar ensamblador en z88dk, embebiendo el código ASM dentro del propio programa.
- printf( “\x1B[%u;%uH”,(21),(1)): Este comando es el equivalente ANSI de gotoxy(x,y), es decir, posiciona el cursor en la posición (1,21) de pantalla para que el próximo printf comience a trazar las letras en esa posición. En este caso lo utilizamos para posicionar en cursor en la parte baja de la pantalla, donde escribimos el título del programa posteriormente.
Dibujar_Gen_Actual()
En cada paso del bucle principal tenemos que redibujar la colonia actual de células. El pseudocódigo para hacer esto es:
Dibujar_Generacion_Actual:
Para todo 'x' y todo 'y':
Si tablero[x][y] = 0: Dibujar Blanco en (x,y)
Si tablero[x][y] = 1: Dibujar Célula en (x,y)
Traducido a código C:
#define DrawCell(x,y,val) \ *((unsigned char *) (0x4000 + 6144 + ((y)<<5) + (x))) = (val)<<3 ; //--- Dibujar en pantalla el array de celulas ------------- void DrawLife( void ) { int x, y; for( y=0; y<ALTO; y++) for( x=0; x<ANCHO; x++) { Celula(x,y) = TempCelula(x,y); DrawCell(x,y,Celula(x,y)); } }
La clave de esta función está en la macro DrawCell, que es la que efectivamente pinta en pantalla las células. Lo interesante de la función es que no dibuja nada en pantalla, sino que modifica los atributos de la videomemoria para cambiar los “espacios en blanco” que hay en pantalla entre 2 colores diferentes (negro y azul). Concretamente, esta macro lo que hace es modificar los atributos (tinta/papel) de los caracteres de 0,0 a 32,16, accediendo directamente a videomemoria, en la zona de los atributos.
Como veremos en posteriores entregas (donde ya trataremos el tema de los gráficos), los atributos de los caracteres (tinta/papel) de la pantalla están situados en memoria a partir de la dirección 22528 (0x4000 + 6144 = 22528, es decir, tras la videomemoria gráfica de los píxeles de pantalla).
Escribiendo en esas 768 (32×24) posiciones consecutivas de memoria modificamos los atributos de los 32×24 caracteres de la pantalla. La organización es lineal, de forma que en 22528 está el atributo del carácter (0,0), en 22529 el de (1,0), en 22528+31 el de (31,0) y en 22528+32 el de (0,1), y así consecutivamente.
Cuando escribimos un byte en una de esas posiciones estaremos modificando los atributos del caracter (x,y) de la pantalla de forma que:
Direccion_atributos(x,y) = 22528 + (y*32) + x
El byte que escribamos define los atributos con el siguiente formato:
| Bits | Significado |
|---|---|
| 0…2 | tinta (0 a 7, orden de los colores del Spectrum) |
| 3…5 | papel (0 a 7, orden de los colores del Spectrum) |
| 6 | brillo (1 ó 0, con o sin brillo) |
| 7 | flash (1 ó 09, con o sin parpadeo) |
Los colores están definidos igual que se detalla en el manual del Spectrum, es decir:
| Valor | Color |
|---|---|
| 0 | negro |
| 1 | azul |
| 2 | rojo |
| 3 | púrpura o magenta |
| 4 | verde |
| 5 | cyan |
| 6 | amarillo |
| 7 | blanco |
Con los bits indicandos anteriormente, un atributo se construiría con el siguiente código:
atributo = (flash<<7) + (brillo<<6) + (papel<<3) + (tinta);
Por ejemplo, para establecer el caracter (2,5) con color verde (4) sobre fondo rojo (2) y con flash, podemos utilizar el siguiente código:
// memaddr = 22528 + (y*32) + x memaddr = 22528 + (5*32) + 2; // escribir en memaddr (flash<<7)+(brillo<<6)+(papel<<3)+tinta. *memaddr = (1<<7) + (2<<3) + (4);
De este modo podemos activar y desactivar cuadros completos de pantalla modificando su tinta y papel. Este método es mucho más rápido para nuestro programa que dibujar los 8×8 pixels de cada carácter para dibujar o apagar las células (una sóla escritura en memoria modifica el estado de 64 píxeles simultáneamente), y puede servirnos de ejemplo para mostrar cómo modificar los atributos.
Calcular_Siguiente_Gen()
En este momento ya tenemos una función que nos genera una colonia inicial de células (aleatoria), y un bucle principal que redibuja la colonia de células actual en memoria. Lo que falta a continuación es implementar la esencia del algoritmo de John Conway para modificar la colonia de células actual (array mapa[]) y obtener el nuevo estado (array temp[]) para, repitiendo el ciclo una y otra vez, realizar la simulación.
El pseudocódigo es el siguiente:
Calcular_Siguiente_Generación:
Para todo 'x' y todo 'y':
Si la célula es del borde (x=0,y=0,x=ancho,y=alto):
Matamos la célula
Si no:
Contar número de células vecinas.
Si la celda (x,y) actual está habitada:
Si tiene menos de 2 vecinas: Matamos la célula
Si tiene más de 3 vecinas : Matamos la célula
Si no está habitada:
Si tiene 2 ó 3 vecinas : Creamos una célula
El código en C que implemente este algoritmo es:
//--- Funcion donde se simula la vida --------------------- void Life( void ) { int x, y; int vecinos; // Calculamos la siguiente generacion for( y=0; y<ALTO; y++) { for( x=0; x<ANCHO ; x++) { // Las celulas del borde mueren if( x==0 || y==0 || x>ANCHO-2 || y>ALTO-2 ) TempCelula(x,y)=0 ; else { // Obtenemos el numero de celulas vecinas vecinos = 0; vecinos += Celula(x-1,y); vecinos += Celula(x+1,y); vecinos += Celula(x,y-1); vecinos += Celula(x,y+1); vecinos += Celula(x-1,y+1); vecinos += Celula(x-1,y-1); vecinos += Celula(x+1,y-1); vecinos += Celula(x+1,y+1); // reglas para células vivas if( Celula(x,y) == 1 ) { // celulas con 2 ó 3 vecinos sobreviven // y el resto muere if( vecinos == 2 || vecinos == 3 ) TempCelula(x,y) = 1; else TempCelula(x,y) = 0; } // reglas para espacios vacios else { // Espacios vacios con 3 vecinos dan lugar // a una nueva celula if( vecinos == 3 ) TempCelula(x,y) = 1; } // fin else espacios vacios } // fin else borrar celulas del borde } // fin for x } // fin for y }
Para compilar el programa puede utilizarse el siguiente comando:
zcc +zxansi -vn -O1 zxlife.c -o zxlife.bin -lndos bin2tap zxlife.bin zxlife.tap rm -f zcc_opt.def
Si ejecutamos el programa en nuestro Spectrum (o en un emulador) veremos la evolución de las células en tiempo real en nuestra pantalla:
Cada vez que pulsemos 'r' se generará una nueva “remesa” de células para volver a aplicar el algoritmo y ver su evolución.
Optimizaciones del Juego de la Vida
Todos los programas pueden ser optimizados, y zxlife no es una excepción. Como ya se ha mostrado en el ejemplo del cálculo de la posición (x,y) en el array, cambiando una multiplicación por 32 por un desplazamiento binario 5 veces a la izquierda obtenemos un gran incremento de velocidad de ejecución. Este incremento de velocidad es tal porque esa función es llamada muchas veces durante la ejecución del programa. Se demuestra con esto que no por el mero hecho de utilizar C o Ensamblador el programa será más o menos rápido: La velocidad de ejecución del programa reside en que utilicemos los algoritmos adecuados a cada problema; así, desplazar binariamente 5 veces es mucho más rápido que multiplicar por 32, y esa multiplicación sería igual de lenta si la programáramos en ensamblador. De ahí la importancia del diseño del programa y los algoritmos empleados en su implementación.
En el caso de zxlife, podemos también optimizar el código de obtención de nuevas generaciones evitando cálculos innecesarios. Concretamente, cuando contamos las células vecinas podemos evitar calcular la posición de cada célula en cada caso. El código original sin optimizar es:
// Obtenemos el numero de celulas vecinas vecinos = 0; vecinos += Celula(x-1,y); vecinos += Celula(x+1,y); vecinos += Celula(x,y-1); vecinos += Celula(x,y+1); vecinos += Celula(x-1,y+1); vecinos += Celula(x-1,y-1); vecinos += Celula(x+1,y-1); vecinos += Celula(x+1,y+1);
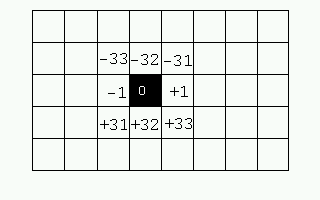
Cada vez que llamamos a Celula(x,y) estamos realizando el cálculo de la posición absoluta de la célula dentro del vector (en nuestra conversión bidimensional a unidimensional) mediante una serie de operaciones matemáticas. Si tenemos en cuenta que todas las células vecinas están a una distancia fija de -1, +2, -33, -32, -31 y +31, +32 y +33 de cada célula, podemos convertir esto a:
offset = (y<<5)+x; // Obtenemos el numero de celulas vecinas vecinos = mapa[ offset-33 ] + mapa[ offset-32 ] + mapa[ offset-31 ] + mapa[ offset-1 ] + mapa[ offset+1 ] + mapa[ offset+31 ] + mapa[ offset+32 ] + mapa[ offset+33 ];
Esto es así porque como podemos ver en la siguiente figura, podemos obtener las 8 células vecinal a partir de un mismo offset calculado:
El código resultante de la optimización sería el siguiente:
//--- Funcion donde se simula la vida --------------------- void Life( void ) { int x, y; unsigned int vecinos, offset; // Calculamos la siguiente generacion for( y=0; y<ALTO; y++) { for( x=0; x<ANCHO ; x++) { // Las celulas del borde mueren if( x==0 || y==0 || x>ANCHO-2 || y>ALTO-2 ) TempCelula(x,y)=0 ; else { offset = (y<<5)+x; // Obtenemos el numero de celulas vecinas vecinos = mapa[ offset-33 ] + mapa[ offset-32 ] + mapa[ offset-31 ] + mapa[ offset-1 ] + mapa[ offset+1 ] + mapa[ offset+31 ] + mapa[ offset+32 ] + mapa[ offset+33 ]; // reglas para células vivas if( mapa[offset] == 1 ) { // celulas con 2 ó 3 vecinos sobreviven // y el resto muere temp[offset] = 0; if( vecinos == 2 || vecinos == 3 ) temp[offset] = 1; } // reglas para espacios vacios else { // Espacios vacios con 3 vecinos dan lugar // a una nueva celula if( vecinos == 3 ) temp[ offset ] = 1; } // fin else espacios vacios } // fin else borrar celulas del borde } // fin for x } // fin for y }
Aparte de la optimización de la función de cálculo de nuevas generaciones, también podemos optimizar la función que dibuja en pantalla de forma que en lugar de realizar el cálculo de posición del atributo en cada célula, lo realice una sola vez y vaya incrementándolo (algo parecido a lo que hemos hecho con el cálculo de células vecinas). Podemos ver la versión optimizada a continuación:
//--- Dibujar en pantalla el array de celulas ------------- void DrawLife( void ) { int i; unsigned char *memaddr; memaddr = (0x4000 + 6144); for( i=0; i<ANCHO*ALTO; i++ ) { mapa[i] = temp[i]; // Dibujamos en pantalla cambiando el ATTR *memaddr = (temp[i]<<4); // pasamos al siguiente caracter en pantalla memaddr++; } }
Lo que hacemos en el ejemplo anterior es apuntar nuestra variable puntero memaddr a la posición de memoria donde comienzan los atributos (memaddr = posición de memoria del atributo del caracter 0,0 de pantalla), tras lo cual podemos escribir el atributo e incrementar el puntero para pasar al siguiente atributo que vamos a modificar. De este modo podemos redibujar nuestros 32×16 caracteres sin tener que recalcular memaddr para cada célula, como se hacía en el caso anterior.
En el fichero comprimido que acompaña a este artículo están almacenadas las 2 versiones de zxlife: la versión 1 (zxlife.c y zxlife.tap) que es la versión original del programa, y la versión 2 (zxlife2.c y zxlife2.tap) que es la versión optimizada con los cambios que hemos explicado en esta sección.
En conclusión
Con el ejemplo de esta entrega hemos pretendido mostrar un ejemplo completo y práctico de cómo z88dk nos puede ayudar a implementar cualquier tipo de programa o algoritmo que deseemos fácilmente (zxlife.c tiene apenas 200 líneas de código contando comentarios y ha sido programado en apenas 30 minutos). Además, se ha podido ver cómo lo importante no es el lenguaje de programación utilizado, sino los algoritmos que se empleen. Por supuesto, zxlife puede optimizarse más aún: no se ha hecho porque el objetivo es que el programa fuera comprensible para los lectores, pero podemos combinar la potencia de C con funciones en ensamblador en aquellos puntos donde se considere oportuno, o utilizar una implementación diferente del algoritmo para calcular las generaciones de células, obteniendo mejores resultados.
En las próximas entregas comenzaremos a hablar de gráficos en el Spectrum, de forma que podamos comenzar a aplicar nuestros conocimientos de z88dk para hacer ya cosas visibles (gráficamente) en nuestro Spectrum.
Listado completo del programa
/* * ZX-Life -> Implementacion de ejemplo en C-z88dk del * simulador de vida de John Conway para * MagazineZX (articulo programacion z88dk). * * v 1.0 (c) 2004 Santiago Romero AkA NoP / Compiler * sromero@gmail.com */ #include "stdio.h" #include "stdlib.h" #include "time.h" #include "string.h" //--- Variables y funciones utilizadas -------------------- #define ANCHO 32 #define ALTO 16 #define NUM_CELULAS 80 char mapa[ANCHO*ALTO], temp[ANCHO*ALTO]; unsigned char *memoffset; unsigned char my_tmp_border; #define Celula(x,y) (mapa[((y)<<5)+(x)]) #define TempCelula(x,y) (temp[((y)<<5)+(x)]) #define DrawCell(x,y,val) \ *((unsigned char *) (0x4000 + 6144 + ((y)<<5) + (x))) = (val)<<3 ; void GenLife( void ); void DrawLife( void ); void Life( void ); void CLS( int value ); void BORDER( unsigned char value ); //--- Funcion principal main() ---------------------------- int main( void ) { int i; GenLife(); while(1) { DrawLife(); Life(); if( getk() == 'r' ) GenLife(); } return(0); } //--- Rellenar el tablero con valores aleat. -------------- void GenLife( void ) { int x, y, i; // Inicializar la semilla de numeros aleatorios srand(clock()); BORDER(0); CLS(0); printf( "\x1B[%u;%uH",(21),(1)); printf(" ZX-Life - MagazineZX - z88dk "); printf(" (r) = nueva generacion aleatoria "); // limpiamos el tablero de celulas for( i=0; i<ALTO*ANCHO; i++) mapa[i] = temp[i] = 0; // generamos unas cuantas celulas aleatorias for( i=0; i< NUM_CELULAS; i++) { x = (rand() % (ANCHO-2)) +1; y = (rand() % (ALTO-2)) +1; TempCelula(x,y) = Celula(x,y) = 1; } } //--- Funcion donde se simula la vida --------------------- void Life( void ) { int x, y; int vecinos; // Calculamos la siguiente generacion for( y=0; y<ALTO; y++) { for( x=0; x<ANCHO ; x++) { // Las celulas del borde mueren if( x==0 || y==0 || x>ANCHO-2 || y>ALTO-2 ) TempCelula(x,y)=0 ; else { // Obtenemos el numero de celulas vecinas vecinos = 0; vecinos += Celula(x-1,y); vecinos += Celula(x+1,y); vecinos += Celula(x,y-1); vecinos += Celula(x,y+1); vecinos += Celula(x-1,y+1); vecinos += Celula(x-1,y-1); vecinos += Celula(x+1,y-1); vecinos += Celula(x+1,y+1); // reglas para células vivas if( Celula(x,y) == 1 ) { // celulas con 2 ó 3 vecinos sobreviven // y el resto muere if( vecinos == 2 || vecinos == 3 ) TempCelula(x,y) = 1; else TempCelula(x,y) = 0; } // reglas para espacios vacios else { // Espacios vacios con 3 vecinos dan lugar // a una nueva celula if( vecinos == 3 ) TempCelula(x,y) = 1; } // fin else espacios vacios } // fin else borrar celulas del borde } // fin for x } // fin for y } //--- Dibujar en pantalla el array de celulas ------------- void DrawLife( void ) { int x, y; for( y=0; y<ALTO; y++) for( x=0; x<ANCHO; x++) { Celula(x,y) = TempCelula(x,y); DrawCell(x,y,Celula(x,y)); } } //--- Borrar la pantalla accediendo a la VRAM ------------- void CLS( int value ) { #asm ld hl, 2 add hl, sp ld a, (hl) ld hl, 16384 ld (hl), a ld de, 16385 ld bc, 6911 ldir #endasm } //--- Cambiar el borde de la pantalla --------------------- void BORDER( unsigned char value ) { my_tmp_border = value<<3; #asm ld hl, 2 add hl, sp ld a, (hl) ld c, 254 out (c), a ld hl, 23624 ld a, (_my_tmp_border) ld (hl), a #endasm }