Aritmética con el Z80
El Z80 nos provee de funciones aritméticas de 8 bits básicas, como son ADD, ADC, SUB, SBC, NEG, CPL y DAA, así como instrucciones para rotación/desplazamiento de bits como RLC, RRC, RL, RR, RLA, RRA, RLCA, RRCA, RLD, RRD, SRA, SLA y SRL.
En muchas de estas operaciones toma especial relevancia CF (el Carry Flag), que podemos modificar mediante SCF y CCF (o realizando atajos como AND A o OR A para sustituir a CCF).
Pero no incluye, como sí lo hacen microprocesadores más avanzados o más modernos, instrucciones para realizar multiplicaciones, divisiones u otras operaciones más complejas.
Esas operaciones ariméticas y matemáticas deberemos crearlas como rutinas utilizando como base las operaciones básicas que acabamos de nombrar, en conjunción con bucles y algoritmos matemáticos o lógicos que nos ayuden a realizarlas.
En este capítulo vamos a ver rutinas para realizar este tipo de operaciones extraídas de diferentes fuentes (libros, webs dedicadas al Z80, foros de desarrollo, canales de discusión sobre programación en ensamblador), de forma que las podamos incorporar directamente en nuestros programas.
En algunas ocasiones se incluirán comentarios sobre cómo opera esta rutina, y en otras simplemente citaremos la rutina con sus parámetros de entrada y salida para poder usarla en nuestros programas. Para toda rutina, se citará la fuente de la que se ha extraído si es conocida, y su autor (si es posible) para darle su merecido crédito por ella.
Las rutinas se reproducen tal cual aparecen en la web, por lo que es posible que alguna de ellas incluyan varios PUSH y POP para preservar registros, y otras no lo hagan. Debido a esto, cuando vayamos a incorporarlas en nuestros programas o librerías se recomienda que se revise la rutina para añadir o quitar la preservación de registros según la necesitemos o no.
Se recomienda al lector que se desarrolle su propia librería aritmetica.asm con una selección de rutinas de esta página, eligiendo aquellas rutinas que pueda necesitar en sus programas, y las aproveche en lugar de intentar “reinventar la rueda” y escribir rutinas de aritmética que puedan ser más lentas que las presentadas.
Sumas y restas de 8 y 16 bits
En el capítulo dedicado a las instrucciones ariméticas básicas (ADD, ADC, SUB y SBC) hemos visto cómo realizar sumas y restas de 8 y 16 bits, apoyándonos en el Carry Flag para ello. Veamos unos ejemplos:
; Sumas de 8 bits add a, b ; A = A+B add a, 70 ; A = A+70 ; Sumas de 16 bits add hl, bc ; HL = HL+BC ; add hl, 1000 ; Instrucción NO VALIDA ; Restas de 8 bits sub b ; A = A-B sub 5 ; A = A-5 ; Restas de 16 bits or a ; Carry Flag = 0 (más rápido que 'ccf') ld hl, 2000 ld bc, 1000 sbc hl, bc ; HL = HL-BC = 2000-1000 = 1000 ; Sumas de registros de 8 bits a registros de 16 bits: OPCION 1 ; HL = HL + A = HL + BC haciendo B = 0 y C = A ld b, 0 ld c, a add hl, bc ; HL = HL+A ; Sumas de registros de 8 bits a registros de 16 bits: OPCION 2 ; HL = HL + A add a, l ld l, a adc a, h ; Esta línea y la siguiente incrementan sub l ; H si el Carry Flag se ha puesto a 1. ld h, a ; HL = HL+A con 2 ciclos menos y no usa BC ; pero ocupa un byte más.
Multiplicar y dividir por potencias de 2
Aunque vamos a ver en un apartado posterior rutinas para realizar multiplicaciones y divisiones “genéricas” (entre dos valores cualquiera), empecemos por estudiar un caso concreto de las multiplicaciones y divisiones, que son cuando la operación se realiza por una potencia de dos (multiplicar/dividir por 2, 4, 8, 16, 32, 64, 128, etc).
Estas multiplicaciones son importantes porque al contrario que las genéricas, que se basan en algoritmos con bucles, utilizan para ello simples instrucciones de desplazamiento de bits y por tanto son mucho más rápidas para el procesador que las multiplicaciones normales.
Si nuestra operación es directamente por una potencia de dos, o se puede convertir en una potencia de dos, es muy recomendable que la realicemos por este método y no usando la rutina de multiplicación/división que tengamos en nuestro programa. Un ejemplo de esto, cuando trabajemos con atributos o con posiciones de texto de pantalla y tengamos que realizar multiplicaciones por 32 (como son las 32 columnas de pantalla), de la misma forma que para muchas tareas en los juegos habrá multiplicaciones por potencias de 2 como 2, 4, 8 ó 16.
El truco para multiplicar por la base lo conocemos desde Educación Primaria ya que es muy sencillo de usar y rápido de calcular: en los números decimales (base 10), añadir un cero a la derecha de un número equivale a multiplicar por 10. Así, si tenemos el número 5 y lo queremos multiplicar por 10 (la base), basta añadir un cero por la derecha (50) y la multiplicación es inmediata sin tener que hacer ningún cálculo de multiplicación.
Si queremos multiplicar por 100 (10^2, simplemente repetimos la operación, volviendo a añadir otro cero. Para multiplicar por 1000 (10^3) de nuevo basta con añadir otro cero.
Añadir un cero a la derecha en la práctica lo que significa es que “desplazamos” el número actual a la izquierda y en el hueco que queda, donde antes estaba el último dígito, añadimos un 0.
Pues bien, en los números binarios ocurre lo mismo con su base: el añadir un cero a la derecha implica multiplicar por la base, es decir, multiplicar por 2:
%00000101 = 5
=> Desplazamos 1 bit a la izquierda
%0000101_
=> Añadimos un 0 en el hueco
%00001010 = 10 (5*2)
=> el bit saliente (7) se va al CARRY FLAG.
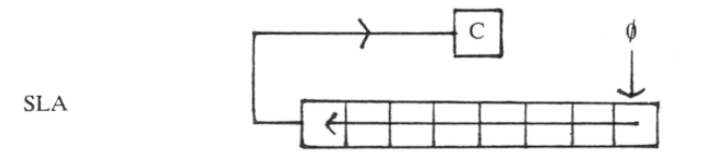
La forma de añadir un cero a un número binario es rotarlo a la izquierda (operación «) y que entre un cero por la derecha. Eso se consigue con las instrucciones desplazamiento SLA r, con un registro de 8 bits como operando:
ld b, 5 sla b ; B = B << 1 = B * 2 = 10
El bit 7 del registro desplazado (que “sale” del registro) se copia en el Carry Flag para que no se pierda, y podamos usarlo para realizar operaciones combinadas de 16 bits.
Múltiples desplazamientos a la izquierda equivalen a multiplicar por 2, por 4, por 8, etc, por lo que si queremos multiplicar el registro B por 8, podemos hacer:
ld b, 5 sla b ; B = B<<1 = B * 2 = 10 sla b ; B = B<<1 = B * 2 = 20 sla b ; B = B<<1 = B * 2 = 40 ; B = B<<3 = B * 8
Así, una sola rotación a la izquierda es multiplicar por 2^1 = 2, dos rotaciones es multiplicar por 2^2 = 4, tres rotaciones por 2^3 = 8, etc.
Optimización para la multiplicación mediante el uso de A:
La operación sla ocupa 2 bytes y tarda 8 ciclos de reloj en ejecutarse, por lo que si lo que queremos multiplicar por una potencia de 2 es el registro A, lo podemos hacer más rápido con múltiples sumas, ya que add a, a ocupa un sólo byte y tarda 4 ciclos:
ld a, 5 add a, a ; A = A*2 = 10 add a, a ; A = (A*2)*2 = A*4 = 20 add a, a ; A = (A*4)*2 = A*8 = 40 ; A = A*8
Podemos combinar multiplicaciones por 2 para lograr multiplicaciones por valores diferentes que sean suma de potencias de dos.
Esta técnica no está limitada a multiplicar sólo por 2, 4, 8, 16, 32, etc. Podemos multiplicar por valores cercanos a estos números, o por combinaciones de potencias de 2 usando sumas o restas del valor original.
Por ejemplo, multiplicar por 5 un valor equivale a multiplicar ese valor por 4 y sumar el valor:
N = N*5 => N = N*5 + N
De modo que multiplicar el valor de A por 5 sería:
ld b, a ; guardamos en B una copia del valor add a, a ; A = A*2 add a, a ; A = A*4 add a, b ; A = A*4 + B = A*5
Del mismo modo, podríamos multiplicar por 6 sumando 2 veces B, por ejemplo. Y podríamos multiplicar por 15 haciendo 4 desplazamientos (A*16) y restando el valor original.
Para valores más complejos, podemos componer “desplazamientos”. Por ejemplo, supongamos que queremos multiplicar el valor de registro por 20. A*20 es lo mismo que A*16 + A*4
ld a, 5 ; Multiplicar 5 por 20 (A * 20 = A * 16 + A * 4) add a, a ; A = A * 2 add a, a ; A = A * 4 ld b, a ; Guardamos B = A*4 add a, a ; A = (A*4)*2 = A * 8 add a, a ; A = (A*8)*2 = A * 16 add a, b ; A = A+B = (A*16) + (A*4) = A*20
Si hubiéramos necesitado multiplicar por 21 o por 19 (por ejemplo), podríamos haber guardado el valor de A antes de este proceso (por ejemplo en el registro C) y haber después sumado o restado C a la multiplicación por 20 para encontrar el valor deseado. Para multiplicar por 22 o por 18 podríamos haberlo sumado o restado 2 veces al resultado, etc.
Pero volvamos a SLA para multiplicar por potencias de 2. Hemos dicho que cada vez que multiplicamos con desplazamientos (o con sumas de A), el bit más significativo (bit 7) pasa al Carry Flag. Si hacemos múltiples operaciones sin utilizar ese bit lo “perdemos”, ya que el máximo valor que podemos almacenar en A es 255, así que no podemos multiplicar números muy grandes. Para valores grandes necesitaremos usar una pareja de registros de 16 bits, e ir pasando el bit saliente (el Carry Flag) al registro de la parte alta del valor:
sla e ; Multiplicamos E por 2 (<<1 y bit 7 pasa al CF) rl d ; Rotamos D metiendo el CF por la derecha.
Al igual que pasaba con ADD A, A, las sumas de 16 bits con ADD HL, HL pueden llegar a ser más rápidas (1 byte, y 11 ciclos de reloj) que la combinación de SLA + RL (4 bytes y 16 ciclos).
Por ejemplo:
; HL = HL * 2 add hl, hl ; HL = HL * 2 ; HL = HL * 8 add hl, hl ; HL = HL*2 add hl, hl ; HL = HL*4 add hl, hl ; HL = HL*8 ; HL = HL * 3 ld c,l ld b,h ; BC = HL add hl,hl ; HL = HL*2 add hl,bc ; HL = HL+BC = HL*3 ; HL = HL * 6 => HL*4 + HL*2 add hl, hl ; HL = HL*2 ld c, l ld b, h ; BC = HL*2 add hl, hl ; HL = HL*4 add hl, bc ; HL = HL+BC = HL*6
Dividiendo por potencias de dos
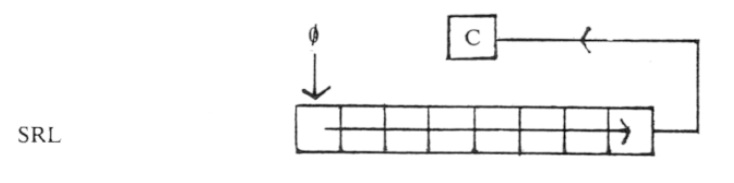
Del mismo modo que desplazar a la izquierda es multiplicar, entonces los desplazamientos a la derecha equivalen a dividir por potencias de 2 (2, 4, 8…), mediante la instrucción SRL:
ld b, 31 srl b ; B = B/2 = 15 srl b ; B = B/4 = 7 (el resto se pierde)
Para dividir registros de 16 bits, lo haremos apoyándonos en el Carry Flag y con RR para la parte baja, al revés como se hacía la multiplicación (ya que tenemos que introducir el bit saliente de D, el bit 0, en vez del bit 7 como en las multiplicaciones):
srl d rr e
Multiplicaciones
El Z80 no tiene opcodes para multiplicar, de modo que tenemos que crearnos una rutina nosotros mismos.
Nuestra primera aproximación (funcional, pero ineficiente) a las multiplicaciones sería utilizar múltiples sumas para ello.
Por ejemplo, podríamos multiplicar D * E realizando D sumas del valor E (o E sumas del valor D) en un registro:
; Multiplicar D*E y dejar el resultado en HL HL_DxE: ld hl, 0 ; HL = 0 (lo usaremos para acumular las sumas) ld a, d or a ; Si el factor que usaremos en el bucle es 0... ret z ; fin de la rutina, retornará con HL = 0 ld b, d ; ponemos un factor como bucle ld d, h ; ponemos d = 0 hldxe_MulLoop: ; HL = HL + DE un total de B veces add hl, de djnz hldxe_MulLoop ret
De la misma forma, una rutina de división se podría basar en múltiples restas.
El problema de las rutinas basadas en bucles es que son lentas y que su tiempo de ejecución depende de los operandos. Si queremos multiplicar por 5 haremos la mitad de iteraciones del bucle que si multiplicamos por 10, por ejemplo.
Para evitar eso, se utilizan rutinas basadas en “rotaciones”, utilizando un algoritmo para ello, igual que hacemos los humanos cuando multiplicamos con números decimales haciendo multiplicaciones pequeñas (de un sólo dígito), desplazando los números a la izquierda para finalmente sumarlos:
4368
x 579
------------
39312
30576
21840
------------
2529072
Cuando presentamos nuestra “librería de funciones útiles” utils.asm vimos que en la ROM del Spectrum ya existe una rutina disponible para multiplicar HL*DE ($30A9, THE 'HL=HL*DE' SUBROUTINE):
HL_HLxDE:
push bc ; BC is saved.
ld b, $10 ; It is to be a 16-bit multiplication.
ld a, h ; A holds the high byte.
ld c, l ; C holds the low byte.
ld hl, $0000 ; Initialise the result to zero.
hl_loop:
add hl, hl ; Double the result.
jr c, hl_end ; Jump if overflow.
rl c ; Rotate bit 7 of C into the carry.
rla ; Rotate the carry bit into bit 0 and bit 7 into the CF.
jr nc, hl_again ; Jump if the carry flag is reset.
add hl, de ; Otherwise add DE in once.
jr c, hl_end ; Jump if overflow.
hl_again:
djnz hl_loop ; Repeat until 16 passes have been made.
hl_end:
pop bc ; Restore BC.
ret
Sin embargo, vamos a ver y utlizar en su lugar una serie de rutinas extraídas de la web MSX Assembly Page, basadas en rotaciones, que podemos añadir a nuestros programas.
Existen diferentes formas de enfocar las rutinas para multiplicar, por lo que podemos encontrar diferentes implementaciones con tiempos de ejecución diferentes, que son más rápidas con ciertos conjuntos de números (por ejemplo, números pequeños), etc. Como se puede ver, hay diferentes rutinas según si queremos multiplicar valores de 8*8 bits, 8*16 bits, o 16*16 bits que ya el algoritmo se puede optimizar para cada caso (y usar menos registros).
;;; Left rotation multiplication: ;;; Their speed is basically quite constant, although depending on the number ;;; of 1’s in the primary multiplier there may be a slight difference in speed ;;; (a 1 usually takes 7 states longer to process than a 0). ;;; ;;; From: https://map.grauw.nl/articles/mult_div_shifts.php ; ; Multiply 8-bit values ; In: Multiply H with E ; Out: HL = result ; Mult8: ld d, 0 ld l, d ld b, 8 Mult8_Loop: add hl, hl jr nc, Mult8_NoAdd add hl, de Mult8_NoAdd: djnz Mult8_Loop ret ; ; Multiply 8-bit value with a 16-bit value ; In: Multiply A with DE ; Out: HL = result ; Mult12: ld l, 0 ld b, 8 Mult12_Loop: add hl, hl add a, a jr nc, Mult12_NoAdd add hl, de Mult12_NoAdd: djnz Mult12_Loop ret ; ; Multiply 16-bit values (with 16-bit result) ; In: Multiply BC with DE ; Out: HL = result ; Mult16: ld a, b ld b, 16 Mult16_Loop: add hl, hl sla c rla jr nc, Mult16_NoAdd add hl, de Mult16_NoAdd: djnz Mult16_Loop ret ; ; Multiply 16-bit values (with 32-bit result) ; In: Multiply BC with DE ; Out: BCHL = result ; Mult32: ld a, c ld c, b ld hl, 0 ld b, 16 Mult32_Loop: add hl, hl rla rl c jr nc, Mult32_NoAdd add hl, de adc a, 0 jp nc, Mult32_NoAdd inc c Mult32_NoAdd: djnz Mult32_Loop ld b, c ld c, a ret
El mismo autor nos muestra una versión de la rutina de multiplicación, pero “desenrollando” los bucles para que sea más rápida:
;;; Unrolled left-rotating multiplication ;;; Quite compact (41 bytes). Takes 268 T-states on average (M1 waits included). ;;; The minimum is 235 states, and the maximum is 301 ticks. ;;; ;;; From: https://map.grauw.nl/articles/mult_div_shifts.php ; ; Multiply 8-bit value with a 16-bit value (unrolled) ; In: Multiply A with DE ; Out: HL = result ; Mult12U: ld l, 0 add a, a jr nc, Mult12U_NoAdd0 add hl, de Mult12U_NoAdd0: add hl, hl add a, a jr nc, Mult12U_NoAdd1 add hl, de Mult12U_NoAdd1: add hl, hl add a, a jr nc, Mult12U_NoAdd2 add hl, de Mult12U_NoAdd2: add hl, hl add a, a jr nc, Mult12U_NoAdd3 add hl, de Mult12U_NoAdd3: add hl, hl add a, a jr nc, Mult12U_NoAdd4 add hl, de Mult12U_NoAdd4: add hl, hl add a, a jr nc, Mult12U_NoAdd5 add hl, de Mult12U_NoAdd5: add hl, hl add a, a jr nc, Mult12U_NoAdd6 add hl, de Mult12U_NoAdd6: add hl, hl add a, a ret nc add hl, de ret
Bastará con incluir estas rutinas en nuestros programas y llamarlas cuando nos sea necesario realizar una multiplicación de dos valores. Como en toda rutina, tenemos que tener en cuenta los registros que modifica y si lo necesitamos, modificarlas para que los preserven y restauren con PUSH y POP.
Divisiones
De la misma forma que se puede multiplicar con múltiples sumas, también podemos dividir de forma poco eficiente con múltiples restas.
Sin embargo, como ocurría con la multiplicación, lo ideal es utilizar algoritmos que no tengan un tiempo de ejecución que dependa linealmente de los valores a dividir.
Mostraremos a continuación unas rutinas finales de división que podemos incluír en nuestros programas.
;;; Fast generic division routines ;;; From: https://map.grauw.nl/articles/mult_div_shifts.php ; ; Divide 8-bit values ; In: Divide E by divider C ; Out: A = result, B = rest ; Div8: xor a ld b, 8 Div8_Loop: rl e rla sub c jr nc, Div8_NoAdd add a, c Div8_NoAdd: djnz Div8_Loop ld b, a ld a, e rla cpl ret ; ; Divide 16-bit values (with 16-bit result) ; In: Divide BC by divider DE ; Out: BC = result, HL = rest ; Thanks to Flyguille for the Div16 routine, ; taken from his MNBIOS sources. Div16: ld hl, 0 ld a, b ld b, 8 Div16_Loop1: rla adc hl, hl sbc hl, de jr nc, Div16_NoAdd1 add hl, de Div16_NoAdd1: djnz Div16_Loop1 rla cpl ld b, a ld a, c ld c, b ld b, 8 Div16_Loop2: rla adc hl, hl sbc hl, de jr nc, Div16_NoAdd2 add hl, de Div16_NoAdd2: djnz Div16_Loop2 rla cpl ld b, c ld c, a ret ; Divide 16 bit value by 8 bit value ; HL = dividend ; C = divisor ; A <- remainder ; C <- divisor ; HL <- quotient Divide16x8: xor a Continue: ld b, 16 d16x8loop: add hl, hl rla jr c, d16x8_overflow ; can be removed for Divide16x7 cp c jr c, d16x8_zerodigit d16x8_overflow: inc l sub c d16x8_zerodigit: djnz d16x8loop ret
Módulo
La operación módulo no es más que el “resto” de la división, de modo que podemos aprovechar las rutinas de división del apartado anterior y descartar el resultado de la misma, utilizando el resto devuelvo por la rutina.
Raíz cuadrada
A continuación se muestra, lista para usar, una rutina de Ricardo Bittencourt para obtener la raíz cuadrada del valor contenido en el registro HL.
;;; Square root routine ;;; Written by Ricardo Bittencourt. ; ; Square root of 16-bit value ; In: HL = value ; Out: D = result (rounded down) ; Sqr16: ld de, $0040 ld a, l ld l, h ld h, d or a ld b, 8 Sqr16_Loop: sbc hl, de jr nc, Sqr16_Skip add hl, de Sqr16_Skip: ccf rl d add a, a adc hl, hl add a, a adc hl, hl djnz Sqr16_Loop ret
Números aleatorios
Si hay una funcionalidad que necesitaremos casi con total seguridad para desarrollar un juego es la posibilidad de generar números aleatorios. Si queremos que cada partida sea diferente y que ciertas acciones varíen (como por ejemplo, que en un juego de puzzle no aparezcan siempre las mismas piezas), necesitaremos una fuente de aleatoriedad, una rutina que nos devuelva un número diferente cada vez.
Hay varias formas de generar números aleatorios. La primera de ella es utilizar funciones matemáticas que nos devuelven un número diferente de una sucesión cada vez que la llamamos. El problema de las rutinas aleatorias basadas en fórmulas es que la sucesión de números aleatorios suele ser cíclico, es decir, que siempre proporcionan los mismos números y en el mismo orden, a partir de una determinada semilla.
Veamos una rutina muy simple (extraída de la página Z80 bits, de Milos Bazelides), que utiliza la fórmula x[i + 1] = (5 * x[i] + 1) mod 256. Es muy simple y de reducido tamaño, pero la serie resultante tiene poca aleatoriedad:
; Rand8 ; Input: none ; Output: A = pseudo-random number, period 256 ; From: https://map.grauw.nl/sources/external/z80bits.html#4.1 RAND8_SEED EQU 0 Rand8: ld a, RAND8_SEED ; Semilla inicial ld b, a add a, a add a, a add a, b inc a ; Otra posibilidad es ADD A, 7 ld (Rand8+1), a ; Código automodificable ret
La rutina utiliza una semilla (RAND_SEED) que inserta en el registro A para realizar una serie de operaciones y generar el siguiente valor de la serie en A.
Al final de la rutina podemos ver cómo hay una instrucción ld (Rand8+1),a la cual modifica el propio código para meter el valor resultante obtenido en el ld a, X inicial. De este modo, la siguiente vez que llamemos a la rutina tendremos en su primer instrucción el último valor generado, que usaremos como origen de los cálculos para obtener el siguiente.
Como la semilla inicial estará definida en el código, esta rutina siempre devolverá la misma secuencia de valores, haciendo que nuestro juego obtenga números aleatorios, pero los mismos en cada partida. Para evitar esto, podemos cambiar el valor de la semilla (alojada en la instrucción ld a, X inicial) con una función como la siguiente:
; A = semilla a utilizar para Rand8 SetRand8Seed: ld (Rand8+1), a ; Establecemos semilla A ret
Y ahora, en nuestro programa, establecer el valor de esa semilla por ejemplo cuando el usuario pulse la tecla para iniciar el juego, y también cambiarla en medio de la partida con valores como por ejemplo: el valor de un determinado registro que no sea el mismo en cada partida, el valor del registro R, o el valor de la parte baja de la variable del sistema FRAMES (que detallaremos en el capítulo dedicado a la ROM del Spectrum):
ld a, r ; El registro R cambia con cada opcode call SetRand8Seed ; Cambiamos la semilla de generación
De la misma forma, la siguiente rutina proporciona un número aleatorio de 16 bits, lo cual hace que la serie de posibles resultados sea mucho mayor (65535 valores) antes de volver a repetir valores de la secuencia.
; Rand16 ; Input: none ; Output: HL = pseudo-random number, period 65536 ; From: https://map.grauw.nl/sources/external/z80bits.html#4.1 RAND16_SEED DW 0 Rand16: ld de, RAND16_SEED ld a, d ld h, e ld l, 253 or a sbc hl, de sbc a, 0 sbc hl, de ld d, 0 sbc a, d ld e, a sbc hl, de jr nc, rand16end inc hl rand16end: ld (Rand16+1), hl ; Código automodificable ret ; HL = semilla a utilizar para Rand16 SetRand16Seed: ld (Rand16+1), hl ; Establecemos semilla HL ret
Aparte de estos 2 ejemplos, hay gran cantidad de rutinas que proporcionan números aleatorios por diferentes métodos.
Una rutina bastante rápida es la basada en el algoritmo Xorshift, de George Marsaglia.
Este algoritmo es el usado por, entre otros, la rutina srand() del compilador de C Z88DK, y es una muy buena rutina generadora de números aleatorios
; Xorshift is a class of pseudorandom number generators discovered ; by George Marsaglia and detailed in his 2003 paper, Xorshift RNGs. ; 16-bit xorshift pseudorandom number generator by John Metcalf ; 20 bytes, 86 cycles (excluding ret) ; returns: hl = pseudorandom number ; corrupts: a ; generates 16-bit pseudorandom numbers with a period of 65535 ; using the xorshift method: ; hl ^= hl << 7 ; hl ^= hl >> 9 ; hl ^= hl << 8 ; some alternative shift triplets which also perform well are: ; 6, 7, 13; 7, 9, 13; 9, 7, 13. SRAND_SEED EQU 1 ; La semilla inicial **NO** debe de ser 0 srand: ld hl, SRAND_SEED ld a, h rra ld a, l rra xor h ld h, a ld a, l rra ld a, h rra xor l ld l, a xor h ld h, a ld (srand+1), hl ; Código automodificable: ; cambiamos la semilla de la primera línea ; de la subrutina, por el último valor ; obtenido. ret ; HL = semilla a utilizar para srand SetSrandSeed: ld (srand+1), hl ; Establecemos semilla HL ret
O la variación de Xorshift implementada por Patrik Rak:
; A = Random Number rnd: ld hl, 0xA280 ; xz -> yw ld de, 0xC0DE ; yw -> zt ld (rnd+1), de ; x = y, z = w ld a, e ; w = w ^ ( w << 3 ) add a, a add a, a add a, a xor e ld e, a ld a, h ; t = x ^ (x << 1) add a, a xor h ld d, a rra ; t = t ^ (t >> 1) ^ w xor d xor e ld h, l ; y = z ld l, a ; w = t ld (rnd+4), hl ret
En el caso del Spectrum algunas rutinas se basan en que la ROM por su naturaleza es “aleatoria” (son 16384 bytes consecutivos de opcodes y datos) salvo algunos bloques concretos donde tenemos zonas vacías, especialmente en la parte superior.
Podríamos haber realizado una rutina básica similar en el Spectrum simplemente usando HL para recoger un dato de la ROM usando el valor actual del registro R (que se incrementa con cada instrucción):
; A = Numero aleatorio 8 bits ; Modifica HL Rand8_ROM: ld a, r ; Algo de aleatoriedad ld l, a ; L = R and %00111111 ; Máscara para acceder a 0-16384 ld h, a ; H = R MOD 16384 ld a, (hl) ; Nuestro número "aleatorio" de 8 bits en A ret ; DE = Numero aleatorio 16 bits ; Modifica A, HL Rand16_ROM: ld a, r ; Algo de aleatoriedad ld l, a ; L = R and %00111111 ; Máscara para acceder a 0-16384 ld h, a ; H = R MOD 16384 ld d, (hl) inc l ld e, (hl) ; Nuestro número "aleatorio" de 16 bits en DE ret
Estas rutinas tienen la desventaja de que dependen de la existencia de la ROM (no valen para desarrollar juegos en cartucho de IF2, donde no hay ROM) y que hay algunas zonas de la rom “vacías” las cuales, si tenemos “mala suerte”, podrían devolver una secuencia continuada del mismo valor (normalmente $FF).
La rutina que veremos a continuación, de la librería libzx de Sebastian Mihai, lo soluciona combinando diferentes métodos (el último número aleatorio devuelto, bytes leídos de la rom, valores de los registros al llamar a la rutina, etc) para obtener en A un número aleatorio de 8 bits:
;------------------------------------------------------- ; random.asm - part of the ZX Spectrum libzx ; library by Sebastian Mihai, 2016 ;------------------------------------------------------- ; our random numbers are, in part, based on reading bytes ; from the 16kb ROM, whose contents are "pretty random": lastRandomNumber db 33 romPointer dw 3 ; Gets an 8-bit random number. ; It is computed using a combination of: ; - the last returned random number ; - a byte from ROM, in increasing order ; - current values of various registers ; - a flat incremented value ; ; Output: ; A - next random number get_next_random: push af push hl ; advance ROM pointer ld hl, romPointer ld c, (hl) inc hl ld b, (hl) ; BC := word (romPointer) ld hl, 3 add hl, bc ; HL := ROM pointer advanced by 3 ld a, h and %00111111 ld h, a ; H := H mod %00111111 ; HL := HL mod 16384, to make sure ; HL points at a ROM location ld (romPointer), hl ; save new location pop hl ; now compute the random number pop bc ; BC := AF rlc c rlc b ld a, (lastRandomNumber) add a, b ; current reg values are "random" add a, c ; so add them in the mix add a, 47 add a, d add a, e add a, h add a, l ld hl, romPointer add a, (hl) ; the contents of the ROM are "random" ; so add it in the mix ld hl, lastRandomNumber ld (hl), a ; save this number ret
En realidad, podríamos llenar un capítulo entero de rutinas diferentes para generar números aleatorios, ya que hay decenas en la red usando diferentes técnicas. Por ahora, podemos utilizar cualquiera de las vistas anteriormente en nuestros programas y obtener una más que decente aleatoriedad, ya que alguna de ellas ha sido utilizada en juegos comerciales reales de la época.
Espejar el registro A
Finalmente, veamos 2 rutinas de WikiTi para “espejar” el registro A, es decir, invertir el orden de los bits, de ABCDEFGH a HGFFEDCBA:
Primero veamos la rutina con el algoritmo que podríamos considerar lógico: con desplazamientos. Ocupa 25 bytes y tarda 96 ciclos de reloj:
; input: b ; output: a ; 25 bytes, 96 clock cycles reverseA: rr b rla rr b rla rr b rla rr b rla rr b rla rr b rla rr b rla rr b rla ret
Sin embargo, como hemos visto en otras rutinas, siempre se pueden abordar los problemas con algoritmos más óptimos con la idea de ahorrar espacio, ahorrar tiempo de ejecución, o ambos. A continuación podemos ver la versión optimizada por calmaniac84 que tarda sólo 66 ciclos de reloj y ocupa 17 bytes:
;- Reverse a ; input: byte in A ; output: Reversed byte in A ; destroys B ; 17 bytes and 66 clock cycles ; author: calcmaniac84 ReverseA: ld b,a ; b=ABCDEFGH rrca ; a=HABCDEFG rrca ; a=GHABCDEF xor b and %10101010 xor b ld b,a ; b=GBADCFEH rrca ; a=HGBADCFE rrca ; a=EHGBADCF rrca ; a=FEHGBADC rrca ; a=CFEHGBAD xor b and %01100110 xor b rrca ; a=HGFEDCBA