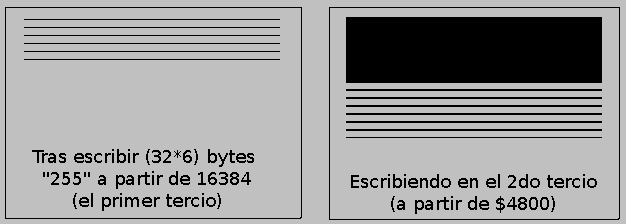
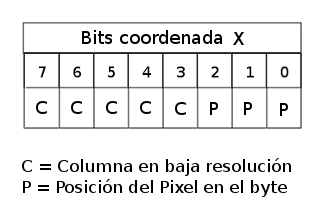
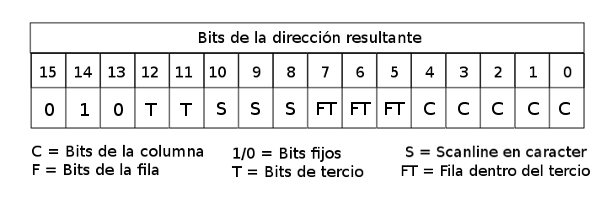
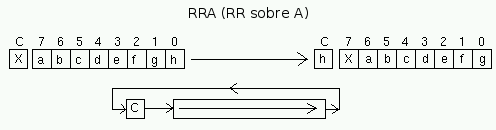
Gráficos (y II): Cálculo de direcciones y coordenadas
En el anterior capítulo exploramos la organización interna de los 6912 bytes de la videomemoria del Spectrum, separándo esta videomemoria en un área de 6144 bytes de archivo de imagen comenzando en la dirección 16384 y otros 768 bytes de archivo de atributos comenzando en la dirección 22528.
La manipulación de dichas áreas de memoria nos permite el trazado de gráficos en pantalla y la manipulación de los colores que tienen dichos gráficos en el monitor. Esto es así porque este área de memoria es leída por el chip de la ULA 50 veces por segundo en sistemas de televisión PAL (Europa y Australia) y 60 veces por segundo en sistemas NTSC (América y Asia) para enviar la señal que el televisor convierte en una imagen para nuestros ojos.
Es necesario que la ULA refresque la pantalla de forma continuada y regular ya que debe reflejar los cambios que los programas hagan en la videomemoria, así cómo para refrescar el estado de los píxeles del monitor (necesario por el funcionamiento de la tecnología CRT).
Sabemos por el capítulo anterior que escribir en la videomemoria nos permite trazar gráficos en pantalla. Hasta ahora hemos visto efectos globales aplicados a toda la vram (borrados, fundidos, etc), pero nuestro interés principal será, seguramente, el trazar gráficos con precisión de bloque o de pixel en la pantalla.
Para poder realizar esta tarea necesitamos relacionar las posiciones de memoria de la videoram con las coordenadas (x,y) de pantalla cuya información gráfica representan. Necesitaremos pues programar rutinas de cálculo de direcciones en función de coordenadas de alta y baja resolución. Sabemos cómo dibujar, pero no cómo calcular la dirección de memoria donde hacerlo. Este es precisamente nuestro objetivo en esta sección.
Para empezar, estableceremos una terminología unánime a la que haremos referencia a lo largo de todo el capítulo, con las siguientes definiciones:
- Resolución del área gráfica: El Spectrum dispone de una resolución de 256×192 píxeles cuyo estado se define en cada byte del área de imagen de la videomemoria.
- Estado de un pixel: Cada byte del área de imagen contiene el estado de 8 píxeles, de tal forma que cada uno de los bits de dicho byte pueden estar a 1 (pixel encendido, se traza con el color de tinta) o a 0 (apagado, se traza con el color del papel).
- Resolución del área de atributos: El Spectrum tiene una resolución de color de 32×24 puntos, que se mapean sobre la pantalla de forma que cada grupo de 8×8 píxeles del área gráfica tiene una correspondencia con un atributo del área de atributos.
- Atributo: Un atributo define en los 8 bits de un byte el color de tinta y papel y el estado de brillo y parpadeo de un bloque concreto de la pantalla.
- Bloque o carácter: Si dividimos la pantalla de 256×192 en 32×24 bloques de color, nos quedan bloques de 8×8 píxeles que mantienen el mismo atributo de pantalla. Estamos acostumbrados a trabajar con bloques ya que el intérprete BASIC del Spectrum utiliza la fuente de la ROM de 8×8 en una rejilla de bloques que coincide con la resolución de atributos. Podemos pensar en los bloques como “posiciones de carácter”.
- Scanline: Un scanline es una línea normalmente horizontal de datos gráficos. Por ejemplo, el scanline 0 de pantalla es la línea gráfica que va desde (0,0) a (255,0), y que definen los 32 bytes de videomemoria que van desde 16384 hasta 16415. También se puede hablar del scanline de un sprite o de un carácter cuando nos referimos a una línea concreta de esa porción de gráfico.
- Coordenadas (x,y): Se utiliza la nomenclatura (x,y) para definir la posición de un píxel en pantalla en función de su posición horizontal y vertical siendo (0,0) la esquina superior izquierda de la misma y (255,191) la esquina inferior derecha. Son, pues, “coordenadas en alta resolución”.
- Coordenadas (c,f): Se utiliza la nomenclatura (c,f), de (columna,fila), para hacer referencia a la posición de un bloque 8×8 en pantalla en función de su posición horizontal y vertical siendo (0,0) la esquina superior izquierda y (31,23) la esquina inferior derecha. Se conocen como “coordenadas en baja resolución” o “coordenadas de bloque” o “de carácter”.
- Conversión (c,f) a (x,y): Como cada bloque es de 8×8 píxeles, podemos convertir una coordenada en baja resolución a coordenadas de pixel como (x,y) = (8*c,8*f). Asímismo, (c,f) = (x/8,y/8).
- Tercio de pantalla: El área gráfica del Spectrum se divide en 3 áreas de 2KB de videoram que almacenan la información de 256×64 píxeles. Estas áreas son comunmente denominadas “tercios”.
- Offset o Desplazamiento: Llamaremos offset o desplazamiento a la cantidad de bytes que tenemos que avanzar desde una base (normalmente el inicio de la propia memoria o un punto de la misma) para llegar a una posición de memoria. Así, un offset de 32 bytes desde 16384 referenciará a los 8 píxeles desde (0,1) a (7,1). En las rutinas que veremos, el offset estará calculado con $0000 como la base, es decir, serán offsets absolutos (posiciones de memoria).
Con estas definiciones, podemos hacer las siguientes afirmaciones:
- La pantalla del Spectrum tiene 192 scanlines horizontales de 256 píxeles cada uno.
- La pantalla del Spectrum se divide en 32×24 bloques o posiciones de caracteres.
- Un bloque o carácter tiene 8 scanlines de 8 píxeles cada uno (8×8).
- Cada byte de la videoram almacena el estado de 8 píxeles, por lo que un bloque se almacena en 8×8/8 = 8 bytes.
- Cada posición de bloque / carácter de la pantalla tiene asociado un atributo del área de atributos.
- Cada uno de los 3 tercios de la pantalla tiene 8 líneas de 32 caracteres.
Para aprovechar la información que trataremos en este capítulo es imprescindible comprender a la perfección la organización interna de la videomemoria que se detalló en el anterior capítulo.
A modo de resumen, la estructura interna de estas 2 áreas de memoria es la siguiente:
- Área de imagen:
- El área de imagen se divide en 3 tercios de pantalla de 2KB de memoria cada uno, que van de $4000 a $47ff (tercio superior), de $4800 a $4fff (tercio central) y de $5000 a $57ff (tercio inferior).
- Cada uno de los tercios comprende 8 líneas de 32 bloques horizontales (256×64 píxeles). Dentro de cada uno de esos 2KB, tenemos, de forma lineal, 64 bloques de 32 bytes (256 píxeles) de información que representan cada scanline de esos 8 bloques.
- Los primeros 32 bytes de dicho bloque contienen la información del scanline 0 del bloque 0. Avanzando de 32 en 32 bytes tenemos los datos del scanline 0 del bloque 1, el scanline 0 del bloque 2, el scanline 0 del bloque 3, etc, hasta que llegamos al scanline 7 del bloque 0. Los siguientes 32 bytes repiten el proceso pero con el scanline 1 de cada bloque.
- Tras los últimos 32 bytes de un tercio, vienen los primeros 32 bytes del siguiente tercio, con la misma organización, pero afectando a otra porción de la pantalla.
- Area de atributos:
- El área de atributos se encuentra en memoria inmediatamente después del área de imagen, por lo que empieza en la posición de memoria 16384+6144 = 22528 ($5800).
- Cada byte del área de atributos se denomina atributo y define el valor de color de tinta, papel, brillo y flash de un carácter / bloque de la pantalla. Esto implica que el área de atributos ocupa 32x24x1 = 768 bytes en memoria, por lo que empieza en 22528 ($5800) y acaba en 23295 ($5aff).
- Los diferentes bits de un atributo de carácter son: Bit 7 = FLASH, Bit 6 = BRIGHT, Bits 5-3 = PAPER, Bits 2-0 = INK.
- Los valores de tinta y papel son un valor de 0-7 que junto al brillo como bit más significativo componen un índice (B-I-I-I) contra una paleta de colores interna definida en la ULA, donde el 0 es el color negro y el 15 el blanco de brillo máximo.
- La organización interna del área de atributos es lineal: Los primeros 32 bytes desde $5800 se corresponden con los atributos de la primera fila de bloques de la pantalla. Los segundos 32 bytes, con la segunda fila, y así sucesivamente hasta los últimos 32 bytes que se corresponden con los atributos de la fila 23. La organización de la zona de atributos no se ve pues relacionada con los tercios de pantalla, tan sólo con la columna y fila (c,f) del bloque.
Nuestro capítulo de hoy tiene los siguientes objetivos prioritarios:
- Cálculo de posiciones de atributo: Saber calcular la posición en memoria del atributo de una posición de carácter (c,f) o de un pixel (x,y).
- Cálculo de posiciones de carácter (baja resolución): Saber calcular la posición en memoria en que comienzan los datos gráficos (pixel 0,0 del carácter) de un carácter o bloque de 8×8 píxeles referenciado como (c,f) o (x,y), asumiendo una resolución de 32×24 bloques en pantalla coincidiendo con las posiciones de carácter de texto estándar.
- Cálculo de posiciones de pixel (alta resolución): Saber calcular la posición en memoria de un pixel referenciado por (x,y).
- Cálculo de posiciones diferenciales: Dada una dirección de memoria de un atributo, carácter o pixel, ser capaz de modificar esta dirección para acceder a los elementos de la izquierda, derecha, arriba o abajo.
Utilizaremos las rutinas que veremos a continuación para el posicionamiento en pantalla de los elementos de nuestros juegos y programas. En los próximos capítulos trabajaremos ya con sprites en baja y alta resolución, fuentes de texto, mapeados por bloques, etc.
Cálculo de posiciones de atributo
Durante el desarrollo de un programa gráfico o un juego necesitaremos (ya sea como funciones independientes o dentro de rutinas de sprites/gráficos más amplias) alguna de las siguientes rutinas:
- Get_Attribute_Offset_LR(c,f) : Dadas las coordenadas en baja resolución (columna,fila) de un bloque / carácter, debe devolver la dirección de memoria del atributo de dicho bloque.
- Get_Attribute_Offset_HR(x,y) : Dadas las coordenadas en alta resolución (x,y) contenida en un bloque / carácter, debe devolver la dirección de memoria del atributo de dicho bloque.
- Get_Attribute_Coordinates_LR(offset): Dada una dirección de memoria dentro del área de atributos, debe devolver las coordenadas (c,f) en baja resolución del bloque al que está asociado.
- Get_Attribute_Coordinates_HR(offset): Dada una dirección de memoria dentro del área de atributos, debe devolver las coordenadas (x,y) en alta resolución del pixel superior izquierdo del bloque al que está asociado.
Es importante comprobar antes de llamar a nuestras rutinas si estas modifican algún registro o flag que necesitemos preservar. Podemos modificar las rutinas para que realicen PUSH y POP de los registros necesarios o hacer nosotros estos PUSH/POP en la rutina llamadora.
Comencemos con las rutinas:
Get_Attribute_Offset
Una primera aproximación a la obtención de la dirección en memoria de un atributo concreto (columna,fila) podría ser la utilización de una tabla de 24 valores de 16 bits que alojara las direcciones de inicio en memoria de los atributos del primer carácter de cada fila.
De esta forma bastaría con utilizar el número de fila como índice en la tabla y sumar el número de columna para obtener la dirección de memoria de la celdilla de atributos de (c,f):
| Línea f | Dirección en Hexadecimal | En Decimal | En Binario |
|---|---|---|---|
| 0 | $5800 | 22528 | 0101100000000000b |
| 1 | $5820 | 22560 | 0101100000100000b |
| 2 | $5840 | 22592 | 0101100001000000b |
| 3 | $5860 | 22624 | 0101100001100000b |
| 4 | $5880 | 22656 | 0101100010000000b |
| 5 | $58a0 | 22688 | 0101100010100000b |
| 6 | $58c0 | 22720 | 0101100011000000b |
| 7 | $58e0 | 22752 | 0101100011100000b |
| 8 | $5900 | 22784 | 0101100100000000b |
| 9 | $5920 | 22816 | 0101100100100000b |
| 10 | $5940 | 22848 | 0101100101000000b |
| 11 | $5960 | 22880 | 0101100101100000b |
| 12 | $5980 | 22912 | 0101100110000000b |
| 13 | $59a0 | 22944 | 0101100110100000b |
| 14 | $59c0 | 22976 | 0101100111000000b |
| 15 | $59e0 | 23008 | 0101100111100000b |
| 16 | $5a00 | 23040 | 0101101000000000b |
| 17 | $5a20 | 23072 | 0101101000100000b |
| 18 | $5a40 | 23104 | 0101101001000000b |
| 19 | $5a60 | 23136 | 0101101001100000b |
| 20 | $5a80 | 23168 | 0101101010000000b |
| 21 | $5aa0 | 23200 | 0101101010100000b |
| 22 | $5ac0 | 23232 | 0101101011000000b |
| 23 | $5ae0 | 23264 | 0101101011100000b |
Direcciones del atributo en el carácter (0,f)
Así pues, podríamos tener una tabla de 16 bytes para indexarla con el número de fila, que permitiría calcular la dirección de memoria como:
dirección_atributo(c,f) = tabla_offsetY_LR[ f ] + c
No obstante, existe una opción mucho más aconsejable en el caso de los atributos como es el realizar el cálculo de la dirección destino en lugar de un lookup en una tabla.
Como ya vimos en el capítulo anterior, la dirección de un atributo concreto se puede calcular mediante la siguiente fórmula:
Direccion_Atributo(x_bloque,y_bloque) = 22528 + (f*32) + c
Desde el inicio del área de atributos, avanzamos 32 bytes por fila hasta posicionarnos en el bloque de 32 bytes que referencia a nuestro bloque, y sumamos el número de columna.
Implementando este cálculo en código máquina, obtendríamos la siguiente rutina (de la cual no haremos uso, ya que diseñaremos una versión mucho más óptima):
;------------------------------------------------------------- ; Obtener la direccion de memoria del atributo del caracter ; (c,f) especificado mediante multiplicacion por 32. ; ; Entrada: B = FILA, C = COLUMNA ; Salida: HL = Direccion del atributo ;------------------------------------------------------------- Get_Attribute_Offset_LR_SLOW: ; calcular dir_atributo como "inicio_attr + (32*f) + c" ld h, 0 ld l, b ; HL = "fila" add hl, hl ; HL = HL*2 add hl, hl ; HL = HL*4 add hl, hl ; HL = HL*8 add hl, hl ; HL = HL*16 add hl, hl ; HL = HL*32 ld d, 0 ld e, c ; DE = "columna" add hl, de ; HL = fila*32 + columna ld de, 22528 ; Direccion de inicio de atributos add hl, de ; HL = 22528 + fila*32 + columna ret
El código que acabamos de ver es perfectamente funcional pero tiene ciertas desventajas:
- Hace uso de prácticamente todo el juego de registros, DE incluído (lo que nos implicaría realizar PUSHes y POPs en nuestra rutina externa o dentro de la misma).
- Tiene un coste de ejecución de 112 t-estados.
Veamos cómo podemos mejorar esta rutina: Si nos fijamos en la representación en binario de la anterior tabla de direcciones, veremos que todas ellas siguen un patrón común:
| Linea f | Dirección en Hexadecimal | En Decimal | En Binario |
|---|---|---|---|
| 0 | $5800 | 22528 | 0101100000000000b |
| 1 | $5820 | 22560 | 0101100000100000b |
| 2 | $5840 | 22592 | 0101100001000000b |
| 3 | $5860 | 22624 | 0101100001100000b |
| 4 | $5880 | 22656 | 0101100010000000b |
| (…) | (…) | (…) | (…) |
| 21 | $5aa0 | 23200 | 0101101010100000b |
| 22 | $5ac0 | 23232 | 0101101011000000b |
| 23 | $5ae0 | 23264 | 0101101011100000b |
- Los 6 bits más significativos de la dirección son 010110, que es la parte de la dirección que provoca que todas las posiciones estén entre $5800 y $5aff.
- Los bits 5, 6, 7 y 8 se corresponden con la fila que queremos consultar.
- Los bits 0, 1, 2, 3 y 4 los utilizaremos para acceder a a la columna deseada. En la tabla anterior son siempre 0 porque estamos mostrando las direcciones de inicio de cada fila, es decir, de (0,f), por lo que estos bits 0-4 son 0.
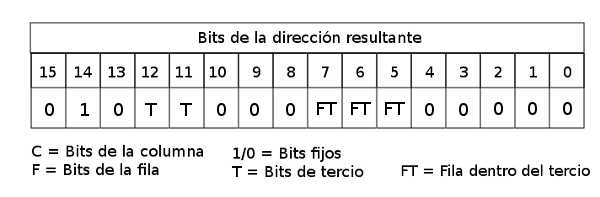
La formación de la dirección destino queda pues así:
Cálculo de la dirección de atributo (c,f)
La rutina de cálculo de la dirección del atributo a partir de coordenadas de baja resolución se podría implementar, pues, de la siguiente forma:
;------------------------------------------------------------- ; Get_Attribute_Offset_LR: ; Obtener la direccion de memoria del atributo del caracter ; (c,f) especificado. Por David Webb. ; ; Entrada: B = FILA, C = COLUMNA ; Salida: HL = Direccion del atributo ;------------------------------------------------------------- Get_Attribute_Offset_LR: ld a, b ; Ponemos en A la fila (000FFFFFb) rrca rrca rrca ; Desplazamos A 3 veces (A=A>>3) and %00000011 ; A = A and %00000011 = los 2 bits mas ; altos de FILA (%000FFFFF -> %000000FF) add a, %01011000 ; Ponemos los bits 15-10 como 010110b ld h, a ; Lo cargamos en el byte alto de HL ld a, b ; Recuperamos de nuevo en A la FILA and %00000111 ; Nos quedamos con los 3 bits que faltan rrca rrca ; Los rotamos para colocarlos en su rrca ; ubicacion final (<<5 = >>3) add a, c ; Sumamos el numero de columna ld l, a ; Lo colocamos en L ret ; HL = %010110FFFFFCCCCC
La rutina realiza operaciones de bits para ubicar los datos de FILA, COLUMNA y 010011b en las posiciones que requiere la dirección destino final. Aconsejamos al lector revisar el capítulo dedicado a Desplazamientos de memoria, bits y operaciones lógicas para recordar el efecto de los desplazamientos realizados con operaciones como RRCA, SRA, SLA, RLC, etc.
El coste de ejecución de esta rutina es de (RET aparte) 70 t-estados y no hace uso de DE, lo que es un ahorro sustancial tanto en tiempo de ejecución como en preservación de un registro muy utilizado.
La salida de esta rutina se puede utilizar directamente para almacenar en (HL) el atributo del caracter (c,f) cuya direccion hemos solicitado:
ld b, 10 ld c, 12 call Get_Attribute_Offset_LR ld a, 85 ; Brillo + Magenta sobre Cyan ld (hl), a ; Establecemos el atributo de (12,10)
La rutina no hace ningún tipo de comprobación del rango de COLUMNA y FILA, por lo que si proporcionamos valores menores de cero o mayores de 31 o 23 respectivamente se devolverá una dirección de memoria fuera del área de atributos.
La versión para coordenadas en alta resolución de la anterior rutina (Get_Attribute_Offset_HR(x,y)) se implementa fácilmente mediante la conversión de las coordenadas (x,y) en coordenadas (c,f) dividiendo x e y entre 8 para obtener las coordenadas de baja resolución que corresponden al pixel que estamos considerando.
Para eso, las primeras líneas de la rutina deberían ser:
srl b srl b srl b ; B = B/8 -> Ahora B es FILA srl c srl c srl c ; C = C/8 -> Ahora C es COLUMNA
Una vez obtenido (c,f), el desarrollo de la rutina es el mismo que en el caso de Get_Attribute_Offset_LR(c,f):
;------------------------------------------------------------- ; Get_Attribute_Offset_HR: ; Obtener la direccion de memoria del atributo del caracter al ; que corresponde el pixel (x,y) especificado. ; ; Entrada: B = Y, C = X ; Salida: HL = Direccion del atributo ;------------------------------------------------------------- Get_Attribute_Offset_HR: srl b srl b srl b ; B = B/8 -> Ahora B es FILA srl c srl c srl c ; C = C/8 -> Ahora C es COLUMNA ld a, b rrca rrca rrca ; Desplazamos A 3 veces (A=A>>3) and %00000011 ; A = A and 00000011 = los 2 bits mas ; altos de FILA (000FFFFFb -> 000000FFb) add a, %01011000 ; Ponemos los bits 15-10 como 010110b ld h, a ; Lo cargamos en el byte alto de HL ld a, b ; Recuperamos de nuevo en A la FILA and %00000011 ; Nos quedamos con los 3 bits que faltan rrca rrca ; Los rotamos para colocarlos en su rrca ; ubicacion final (<<5 = >>3) add a, c ; Sumamos el numero de columna ld l, a ; Lo colocamos en L ret ; HL = 010110FFFFFCCCCCb
Hemos utilizado las instrucciones de desplazamiento SRL sobre los registros B y C para dividir sus valores por 8 y convertir la dirección (x,y) en una dirección (c,f), pudiendo aplicar así el algoritmo de cálculo de dirección que ya conocemos.
Get_Attribute_Coordinates
La siguiente rutina nos proporciona, dada una dirección de memoria apuntada por HL y dentro de la zona de atributos, la posición (c,f) que corresponde a dicho carácter. Se basa en la descomposición de HL en los campos que componen la dirección del atributo:
;------------------------------------------------------------- ; Get_Attribute_Coordinates_LR ; Obtener las coordenadas de caracter que se corresponden a ; una direccion de memoria de atributo. ; ; Entrada: HL = Direccion del atributo ; Salida: B = FILA, C = COLUMNA ;------------------------------------------------------------- Get_Attribute_Coordinates_LR: ; Descomponemos HL = 010110FF FFFCCCCCb ld a, h ; A = 010110FFb and %00000011 ; A = bits 0, 1 de HL = 2 bits altos de F, CF=0 rlca rlca rlca ; Rotacion a izquierda 000000FFb -> 000FF000b ld b, a ; B = 000FF000b ld a, l and %11100000 ; Nos quedamos con los 3 bits mas altos rlca rlca rlca ; Rotacion a izquierda FFF00000b -> 00000FFFb or b ; A = A + B = 000FFFFFb ld b, a ; B = FILA ld a, l and %00011111 ; Nos quedamos con los 5 bits mas bajos ld c, a ; C = COLUMNA ret
De nuevo, el código no incluye ningún tipo de control sobre la dirección que se le proporciona, que podría estar fuera de la zona de atributos y le haría devolver valores en el rango 0-255 para B y para C que, obviamente, no corresponden con la dirección entrada en HL.
La rutina para trabajar con coordenadas en alta resolución (Get_Attribute_Coordinates_HR(x,y)) es esencialmente idéntica a su versión en baja resolución, salvo que finaliza multiplicando B y C por 8 (mediante instrucciones de desplazamiento a izquierda) para convertir las coordenadas (c,f) en (x,y). Los valores (x,y) resultantes se corresponderán con el pixel superior izquierdo del bloque apuntado por (c,f).
;------------------------------------------------------------- ; Get_Attribute_Coordinates_HR ; Obtener las coordenadas de pixel que se corresponden a ; una direccion de memoria de atributo. ; ; Entrada: HL = Direccion del atributo ; Salida: B = y, C = x ;------------------------------------------------------------- Get_Attribute_Coordinates_HR: ; Descomponemos HL = 010110FF FFFCCCCCb ld a, h ; A = 010110FFb and 3 ; A = bits 0, 1 de HL = 2 bits altos de F, CF=0 rlca rlca rlca ; Rotacion a izquierda 000000FFb -> 000FF000b ld b, a ; B = 000FF000b ld a, l and %11100000 ; Nos quedamos con los 3 bits mas altos rlca rlca rlca ; Rotacion a izquierda FFF00000b -> 00000FFFb or b ; A = A + B = 000FFFFFb ld b, a ; B = FILA ld a, l and %00011111 ; Nos quedamos con los 5 bits mas bajos ld c, a ; C = COLUMNA sla c sla c sla c ; C = C*8 sla b sla b sla b ; B = B*8 ret
Cálculo de posiciones diferenciales de atributo
Una vez calculada la posición de memoria de un atributo, puede interesarnos (por ejemplo, en una rutina de impresión de Sprites) el conocer la dirección de memoria del bloque inferior, superior, izquierdo o derecho sin necesidad de recalcular HL a partir de las coordenadas. Por ejemplo, esto sería útil para imprimir los atributos de un sprite de Ancho X Alto caracteres sin recalcular la dirección de memoria para cada atribuo.
Asumiendo que HL contiene una dirección de atributo válida y que tenemos verificado que nuestro sprite no tiene ninguno de sus caracteres fuera del área de pantalla, podemos modificar HL para movernos a cualquiera de los atributos de alrededor. Para eso aprovecharemos la linealidad del área de atributos incrementando o decrementando HL para movernos a izquierda o derecha y sumando o restando 32 a HL para bajar o subir una línea:
Atributo_derecha:
inc hl ; HL = HL + 1
Atributo_izquierda:
dec hl ; HL = HL - 1
Atributo_abajo:
ld de, 32
add hl, de ; HL = HL + 32
Atributo_arriba:
ld de, -32
add hl, de ; HL = HL - 32
Si tenemos la necesidad de preservar el valor del registro DE y el utilizarlo para sumar o restar 32 nos supone hacer un PUSH y POP del mismo a la pila y queremos evitar esto, podemos sumar la parte baja y después incrementar la parte alta si ha habido acarreo:
Atributo_abajo_sin_usar_DE_2:
ld a, l ; A = L
add a, 32 ; Sumamos A = A + 32 . El Carry Flag se ve afectado.
ld l, a ; Guardamos en L (L = L+32)
jr nc, attrab_noinc
inc h
attrab_noinc: ; Ahora HL = (H+CF)*256 + (L+32) = HL + 32
Atributo_arriba_sin_usar_DE:
ld a, l ; A = L
sub 32 ; Restamos A = A - 32 . El Carry Flag se ve afectado.
ld l, a ; Guardamos en L (L = L-32)
jr nc, attrab_nodec
dec h
attrab_nodec: ; Ahora HL = (H+CF)*256 + (L+32) = HL + 32
Nótese que, como nos apunta Jaime Tejedor en los foros de Speccy.org, el código con salto…
jr nc, attrab_noinc inc h attrab_noinc:
… es más rápido que la combinación de ADD y ADC para sumar 32 al byte bajo de HL y 0 + Acarreo al byte alto de HL:
ld a, 0 ; Ponemos A a cero, no podemos usar un "xor a" ; o un "or a" porque afectariamos al Carry Flag. adc a, h ; A = H + CarryFlag ld h, a ; H = H + CarryFlag ; Ahora HL = (H+CF)*256 + (L+32) = HL + 32
Este código no utiliza DE pero se apoya en el registro A para los cálculos. Si necesitamos preservar su valor, siempre podemos realizar un ex af, af' antes y después de la ejecución de la rutina.
Cálculo de posiciones de caracteres
Nuestro siguiente objetivo es el de conocer el mecanismo para trabajar con gráficos de baja resolución o gráficos de bloque / carácter. Esto nos permitirá dibujar gráficos de 8×8 píxeles (o de múltiplos de ese tamaño) comenzando en posiciones de memoria de carácter, en nuestra pantalla de 32×24 bloques de baja resolución.
Para ello necesitamos calcular la dirección de inicio en videomemoria de la dirección de inicio del bloque.
Las rutinas que tenemos que implementar son:
- Get_Char_Offset_LR(c,f) : Dadas las coordenadas en baja resolución (columna,fila) de un bloque / carácter, debe devolver la dirección de memoria de los 8 pixeles del scanline 0 de dicho bloque.
- Get_Char_Offset_HR(x,y) : Dadas las coordenadas en alta resolución (x,y) de un bloque / carácter, debe devolver la dirección de memoria de los 8 pixeles del scanline 0 de dicho bloque.
- Get_Char_Coordinates_LR(offset): Dada una dirección de memoria dentro del área de imagen, debe devolver las coordenadas (c,f) en baja resolución del bloque al que está asociada.
- Get_Char_Coordinates_HR(offset): Dada una dirección de memoria dentro del área de imagen, debe devolver las coordenadas (x,y) en alta resolución del pixel superior izquierdo del bloque al que está asociada.
Nótese que podemos realizar las 2 primeras rutinas de forma que devuelvan el offset calculado bien en el registro DE o bien en el registro HL. Según utilicemos los registros en el código que llama a la rutina, puede sernos más conveniente recibir el valor en uno u otro registro. Si resulta necesario, podemos adaptar el código de las rutinas para que funcionen con uno u otro registro, o utilizar al final de la misma (o tras el call) un EX HL, DE que devuelva el resultado en el registro que más nos interese.
Cálculo de posiciones de caracteres por composición
Utilizando técnicas de composición desde los bits de las coordenadas vamos a calcular la dirección de inicio de cada “primera línea” de fila de caracteres de la pantalla, es decir, el scanline 0 de cada fila de bloques en baja resolución. Conociendo la posición inicial de dicha línea podemos sumar el número de columna y posicionarnos en el inicio del carácter (c,f) deseado, para trazar en él texto o un sprite de 8×8 (o múltiplos).
Al igual que en el caso de las direcciones de atributo, es posible componer la dirección de memoria de este “pixel 0” del “scanline 0” de la fila f mediante descomposición de los bits de las coordenadas y su recomposición en una dirección en memoria.
Para encontrar la relación coordenadas/dirección comencemos viendo una tabla con las direcciones de pantalla buscadas ya precalculadas:
| Linea f | Direccion (0,f) (HEX) | (Decimal) | (Binario) | Tercio (0-2) | Fila dentro del tercio |
|---|---|---|---|---|---|
| 0 | $4000 | 16384 | 0100000000000000b | 0 (00b) | 0 |
| 1 | $4020 | 16416 | 0100000000100000b | 0 (00b) | 1 |
| 2 | $4040 | 16448 | 0100000001000000b | 0 (00b) | 2 |
| 3 | $4060 | 16480 | 0100000001100000b | 0 (00b) | 3 |
| 4 | $4080 | 16512 | 0100000010000000b | 0 (00b) | 4 |
| 5 | $40a0 | 16544 | 0100000010100000b | 0 (00b) | 5 |
| 6 | $40c0 | 16576 | 0100000011000000b | 0 (00b) | 6 |
| 7 | $40e0 | 16608 | 0100000011100000b | 0 (00b) | 7 |
| 8 | $4800 | 18432 | 0100100000000000b | 1 (01b) | 0 |
| 9 | $4820 | 18464 | 0100100000100000b | 1 (01b) | 1 |
| 10 | $4840 | 18496 | 0100100001000000b | 1 (01b) | 2 |
| 11 | $4860 | 18528 | 0100100001100000b | 1 (01b) | 3 |
| 12 | $4880 | 18560 | 0100100010000000b | 1 (01b) | 4 |
| 13 | $48a0 | 18592 | 0100100010100000b | 1 (01b) | 5 |
| 14 | $48c0 | 18624 | 0100100011000000b | 1 (01b) | 6 |
| 15 | $48e0 | 18656 | 0100100011100000b | 1 (01b) | 7 |
| 16 | $5000 | 20480 | 0101000000000000b | 2 (10b) | 0 |
| 17 | $5020 | 20512 | 0101000000100000b | 2 (10b) | 1 |
| 18 | $5040 | 20544 | 0101000001000000b | 2 (10b) | 2 |
| 19 | $5060 | 20576 | 0101000001100000b | 2 (10b) | 3 |
| 20 | $5080 | 20608 | 0101000010000000b | 2 (10b) | 4 |
| 21 | $50a0 | 20640 | 0101000010100000b | 2 (10b) | 5 |
| 22 | $50c0 | 20672 | 0101000011000000b | 2 (10b) | 6 |
| 23 | $50e0 | 20704 | 0101000011100000b | 2 (10b) | 7 |
Examinemos (y marquemos) los bits de la representación binaria de la dirección para una selección de elementos de la tabla:
| Linea f | Direccion (0,f) (HEX) | (Decimal) | (Binario) | Tercio (0-2) | Fila dentro del tercio |
|---|---|---|---|---|---|
| 0 | $4000 | 16384 | 0100000000000000b | 0 (00b) | 0 |
| 1 | $4020 | 16416 | 0100000000100000b | 0 (00b) | 1 |
| 2 | $4040 | 16448 | 0100000001000000b | 0 (00b) | 2 |
| 3 | $4060 | 16480 | 0100000001100000b | 0 (00b) | 3 |
| (…) | (…) | (…) | (…) | (…) | (…) |
| 8 | $4800 | 18432 | 0100100000000000b | 1 (01b) | 0 |
| 9 | $4820 | 18464 | 0100100000100000b | 1 (01b) | 1 |
| 10 | $4840 | 18496 | 0100100001000000b | 1 (01b) | 2 |
| (…) | (…) | (…) | (…) | (…) | (…) |
| 23 | $50e0 | 20704 | 0101000011100000b | 2 (10b) | 7 |
Lo primero que puede llamarnos la atención es lo siguiente:
- Hay una relación directa entre el byte alto de la dirección y el tercio en que está posicionada la línea. Esta relación está marcada por los bits 3 y 4 del byte superior:
- Tercio superior (0, 00b) → Byte alto = $40 → Bits 3 y 4 = 00.
- Tercio central (1, 01b) → Byte alto = $48 → Bits 3 y 4 = 01.
- Tercio inferior (2, 10b) → Byte alto = $50 → Bits 3 y 4 = 10.
- Conclusión: el número de tercio se corresponde con los 2 bits superiores de la coordenada Y, de tal forma que las fila (0,7) están en el tercio 00b, las filas 8-15 en el tercio 01b, y las 16-23 en el 10b.
- Hay una relación directa entre el número de fila dentro de cada tercio (0-7) y los 3 bits superiores (5-7) del byte bajo de la dirección.
- Los 3 bytes más significativos de la dirección son siempre 010b. Esta es la parte de la composición de la dirección que ubica el offset en memoria en el rango de direcciones del área de imagen de la videoram ($4000 a $57ff).
- Los 5 bytes menos significativos de la dirección son siempre cero en la tabla. En realidad, representan a la columna (posición c de carácter dentro de los 32 bytes de datos horizontales) pero al estar calculando direcciones de inicio de línea (c = 0 = 00000b), en nuestro caso son siempre cero.
Así pues, podemos componer la dirección en memoria del pixel (0,0) de un carácter (0,f) de la pantalla como:
Cálculo de la dirección del scanline 0 de (0,f)
A partir del anterior diagrama, se desarrollan las siguientes subrutinas:
Get_Line_Offset
Esta rutina devuelve en HL la dirección de memoria de una fila en baja resolución. Esa dirección apunta a los 8 píxeles (0-7) del scanline 0 de la fila solicitada.
;------------------------------------------------------------- ; Get_Line_Offset_LR(f) ; Obtener la direccion de memoria de inicio de la fila f. ; ; Entrada: B = FILA ; Salida: HL = Direccion de memoria del caracter (0,f) ;------------------------------------------------------------- Get_Line_Offset_LR: ld a, b ; A = B, para extraer los bits de tercio and %00011000 ; A = A and 00011000b ; A = estado de bits de TERCIO desde FILA add a, %01000000 ; Sumamos $40 (bits superiores = 010) ld h, a ; Ya tenemos la parte alta calculada ; H = 010TT000 ld a, b ; Ahora calculamos la parte baja and %00000111 ; Nos quedamos con los bits más bajos de FILA ; que coinciden con FT (Fila dentro del tercio) rrca ; Ahora A = 00000NNNb (donde N=FT) rrca ; Desplazamos A 3 veces rrca ; A = NNN00000b ld l, a ; Lo cargamos en la parte baja de la direccion ret ; HL = 010TT000NNN00000b
Get_Char_Offset
Como ya sabemos, la posición horizontal de un pixel dentro de una fila sí que es lineal, a razón de 8 píxeles por columna, por lo que:
OFFSET(c,f) = Direccion_Inicio(f) + c
y también:
OFFSET(x,y) = Direccion_Inicio(y/8) + (x/8)
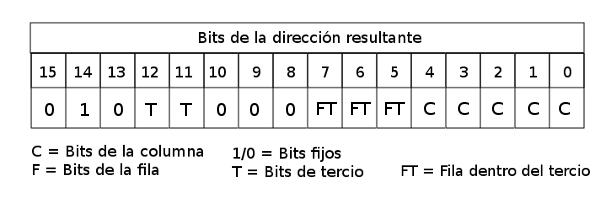
Así, una vez calculado el inicio de línea, basta sumar la columna para obtener la dirección de memoria del scanline 0 del carácter en baja resolución (c,f):
Cálculo de la dirección del scanline 0 de (c,f)
El código con la columna añadida quedaría así:
;------------------------------------------------------------- ; Get_Char_Offset_LR(c,f) ; Obtener la direccion de memoria del caracter (c,f) indicado. ; ; Entrada: B = FILA, C = COLUMNA ; Salida: HL = Direccion de memoria del caracter (c,f) ;------------------------------------------------------------- Get_Char_Offset_LR: ld a, b ; A = B, para extraer los bits de tercio and %00011000 ; A = A and 00011000b ; A = estado de bits de TERCIO desde FILA add a, %01000000 ; Sumamos $40 (bits superiores = 010) ld h, a ; Ya tenemos la parte alta calculada ; H = 010TT000 ld a, b ; Ahora calculamos la parte baja and %00000111 ; Nos quedamos con los bits más bajos de FILA ; que coinciden con FT (Fila dentro del tercio) rrca ; Ahora A = 00000NNNb (N=FT) rrca ; Desplazamos A 3 veces a la derecha rrca ; A = NNN00000b add a, c ; Sumamos COLUMNA -> A = NNNCCCCCb ld l, a ; Lo cargamos en la parte baja de la direccion ret ; HL = 010TT000NNNCCCCCb
Una rutina que deba trabajar con direcciones en alta resolución pero que devuelva el offset del inicio del bloque que contiene el punto (x,y) deberá dividir B y C entre 8 en el punto de entrada de la rutina:
;------------------------------------------------------------- ; Get_Char_Offset_HR(x,y) ; Obtener la direccion de memoria del caracter que contiene ; el pixel (x,y) indicado. ; ; Entrada: B = Y, C = X ; Salida: HL = Direccion de memoria del caracter con (x,y) ;------------------------------------------------------------- Get_Char_Offset_HR: srl b srl b srl b ; B = B/8 -> Ahora B es FILA srl c srl c srl c ; C = C/8 -> Ahora C es COLUMNA (...) ; Resto de la rutina Get_Char_Offset_LR ret
Get_Char_Coordinates
Nuestra siguiente subrutina tiene como objetivo el calcular la posición (c,f) en baja resolución de un carácter dado un offset en memoria que almacene alguno de los 64 pixeles del mismo. Llamar a esta función con la dirección de cualquiera de las 8 líneas de un carácter devolvería el mismo par de coordenadas (c,f):
;------------------------------------------------------------- ; Get_Char_Coordinates_LR(offset) ; Obtener las coordenadas (c,f) que corresponden a una ; direccion de memoria de imagen en baja resolucion. ; ; Entrada: HL = Direccion de memoria del caracter (c,f) ; Salida: B = FILA, C = COLUMNA ;------------------------------------------------------------- Get_Char_Coordinates_LR: ; HL = 010TT000 NNNCCCCCb -> ; Fila = 000TTNNNb y Columna = 000CCCCCb ; Calculo de la fila: ld a, h ; A = H, para extraer los bits de tercio and %00011000 ; A = 000TT000b ld b, a ; B = A = 000TT000b ld a, l ; A = L, para extraer los bits de N (FT) and %0b11100000 ; A = A and 11100000b = NNN00000b rlc a ; Rotamos A 3 veces a la izquierda rlc a rlc a ; A = 00000NNNb or b ; A = A or b = 000TTNNNb ld b, a ; B = A = 000TTNNNb ; Calculo de la columna: ld a, l ; A = L, para extraer los bits de columna and %00011111 ; Nos quedamos con los ultimos 5 bits de L ld c, a ; C = Columna ret ; HL = 010TT000NNNCCCCCb
Adaptar esta rutina a alta resolución (Get_Char_Coordinates_HR(x,y)) implicaría el multiplicar las coordenadas X e Y por 8, añadiendo el siguiente código inmediatamente antes del ret:
sla c sla c sla c ; C = C*8 sla b sla b sla b ; B = B*8
Si no queremos tener una rutina específica para esta operación, podemos llamar a la rutina en baja resolución y realizar los desplazamientos (*8) a la salida de la misma.
Cálculo de posiciones diferenciales de carácter
Recorrer los 8 scanlines de un bloque
Dada en HL la dirección del primer scanline de un bloque, podemos avanzar a lo largo de los 7 scanlines del mismo bloque sumando “256” a dicha dirección. Como sumar 256 equivale a incrementar la parte alta de la dirección, podemos subir y bajar al scanline anterior y siguiente de los 8 que componen el carácter mediante simples dec h e inc h:
Scanline_Arriba_HL: dec h ; H = H - 1 (HL = HL-255) Scanline_Abajo_HL: inc h ; H = H + 1 (HL = HL-255)
Este salto de 256 bytes será válido sólo dentro de los 8 scanlines de un mismo carácter.
Offset del carácter de la izquierda/derecha/arriba/abajo
Dentro de las rutinas de impresión de sprites de más de un carácter es probable que necesitemos movernos a los carácteres de alrededor de uno dado (normalmente hacia la derecha y hacia abajo).
Las siguientes rutinas no realizan control de la posición, por lo que moverse en una dirección cuando estamos en el límite del eje vertical u horizontal tendrá resultados diferentes de los esperados.
Moverse un carácter a derecha o izquierda es sencillo dada la disposición lineal de las filas de caracteres. Estando en el scanline 0 de un carácter, bastará con incrementar o decrementar la posición de memoria actual:
Caracter_Derecha_HL:
inc hl ; HL = HL + 1
Caracter_Izquierda_HL:
dec hl ; HL = HL - 1
Moverse un carácter arriba o abajo es más laborioso ya que tenemos que tener en cuenta los cambios de tercios. Para ello, basta con que recordemos la disposición de los bits de la dirección:
| Bits = | Dirección VRAM | Bits de Tercio | Bits de scanline | Bits de Carácter-Y | Bits de Columna |
|---|---|---|---|---|---|
| HL = | 010 | TT | SSS | NNN | CCCCC |
Así, para saltar al siguiente carácter tenemos que incrementar los 3 bits más altos de L (sumando 32). Esto provocará el avance de bloque en bloque, pero debemos tener en cuenta el momento en que realizamos un salto del bloque 7 al 8, y del 15 al 16, ya que entonces tenemos que cambiar de tercio y poner NNN a 0.
Podemos detectar fácilmente el paso de la fila 7 a la 8 y de la 15 a la 16 ya que en ambos casos la “Fila dentro del Tercio” (NNN, bits 7, 6 y 5 de la dirección) pasaría de 111b a 1000b, lo que provocaría que estos 3 bits se quedaran a 0 y se activara el bit de CARRY.
Es decir, cuando tenemos TT = 00b y NNN = 111b y queremos avanzar al siguiente scanline, sumamos 32 (00100000b) con lo que provocamos NNN = 000b y Carry=1. Teniendo la variable “Fila dentro del Tercio” a 1, basta con que incrementemos TT sumando 00001000b (8) a la parte alta, lo que sumaría 01b a los 2 bits de tercio TT:
El código sería el siguiente:
Caracter_Abajo_HL:
ld a, l ; Cargamos A en L y le sumamos 32 para
add a, %00100000 ; incrementar "Bloque dentro del tercio" (+32)
ld l, a ; L = A
jr nc, no_ajustar_H_abajob ; Si esta suma produce acarreo, ajustar
ld a, h ; la parte alta sumando 8 a H (TT = TT + 1).
add a, %00001000 ; Ahora NNN=000b y TT se ha incrementado.
ld h, a ; H = A
no_ajustar_H_abajob
; Ahora HL apunta al bloque de debajo.
El procedimiento para subir un carácter es similar:
Caracter_Arriba_HL:
ld a, l ; Cargamos L en A
and %11100000 ; A = A and 11100000b
jr nz, nofix_h_arribab ; Si no es cero, no retrocedemos tercio
ld a, h ; Si es cero, ajustamos tercio (-1)
sub %00001000 ; Decrementamos TT
ld h, a
nofix_h_arribab:
ld a, l ; Decrementar NNN
sub 32
ld l, a ; NNN = NNN-1
ret
Con estas 2 subrutinas podemos subir y bajar carácter a carácter sin tener que recalcular la dirección destino y haciendo uso sólo de A, H y L. Hay que tener en cuenta, no obstante, que se no comprueban los límites de la pantalla, por lo que no nos avisarán si pretendemos “subir” más arriba de la línea 0 o “bajar” más abajo de la 23.
Cálculo de posiciones de píxeles
Finalmente, en cuanto a coordenación, vamos a estudiar el cálculo de la dirección de memoria de un pixel (x,y) en alta resolución. La dirección en memoria obtenida tendrá la información gráfica de 8 píxeles (pues cada byte almacena el estado de 8 píxeles horizontales consecutivos). Debido a esto nuestra rutina no sólo deberá devolver el offset en memoria sino un valor de posición relativa 0-7 que nos permita alterar el pixel concreto solicitado.
Nuestra rutina de cálculo de offset puede ser implementada mediante 2 aproximaciones:
- Mediante cálculo de la posición de memoria a partir de las coordenadas (x,y), utilizando operaciones de descomposición y rotación de bits, como ya hemos visto en los apartados anteriores.
- Mediante una tabla precalculada de posiciones de memoria que almacene la dirección de inicio de cada línea de pantalla, a la cual sumaremos el número de columna (x/8), obteniendo así el offset de nuestro pixel.
Vamos a ver las 2 técnicas por separado con rutinas aplicadas a cada uno de los métodos. Cada sistema, como veremos, tiene sus ventajas e inconvenientes, resultando siempre ambos un balance entre el tiempo de ejecución de una rutina y la ocupación en bytes en memoria entre código y datos de la misma.
Las rutinas que tenemos que implementar son:
- Get_Pixel_Offset(x,y) : Dadas las coordenadas en alta resolución (x,y) de un pixel, debe devolver la dirección de memoria que aloja el pixel y un indicador de la posición del pixel dentro de dicho byte (recordemos que cada dirección de memoria contiene los datos de 8 píxeles lineales consecutivos), utilizando descomposición y composición de bits.
- Get_Pixel_Coordinates(offset): Dada una dirección de memoria dentro del área de imagen, debe devolver las coordenadas (x,y) del pixel al que está asociada.
- Get_Pixel_Offset_LUT(x,y) : Dadas las coordenadas en alta resolución (x,y) de un pixel, debe devolver la dirección de memoria que aloja dicho pixel mediante la utilización de tablas de precálculo (Look Up Table, o LUT).
Cálculo de posiciones de pixeles mediante composición
Hasta ahora hemos visto rutinas que nos proporcionan la posición en memoria de un bloque en baja resolución, pero en el caso que veremos ahora tenemos una coordenada Y que se mueve de 0 a 191, por lo que la posición en memoria puede corresponder a cualquiera de los 8 scanlines de un bloque dado. Además, la coordenada X tampoco es un carácter por lo que el pixel resultante es el estado de un bit concreto de la dirección obtenida.
Así pues, ¿cómo podemos calcular la dirección destino del pixel cuando tratamos con coordenadas en alta resolución? Recuperemos para ello parte de nuestra tabla de direcciones de memoria en baja resolución:
| Línea LowRes | Línea HiRes | Direccion (0,f) (HEX) | (Decimal) | (Binario) | Tercio (0-2) | Fila en el tercio |
|---|---|---|---|---|---|---|
| 0 | 0 | $4000 | 16384 | 0100000000000000b | 0 (00b) | 0 |
| 1 | 8 | $4020 | 16416 | 0100000000100000b | 0 (00b) | 1 |
| 2 | 16 | $4040 | 16448 | 0100000001000000b | 0 (00b) | 2 |
| 3 | 24 | $4060 | 16480 | 0100000001100000b | 0 (00b) | 3 |
| (…) | (…) | (…) | (…) | (…) | (…) | (…) |
Añadamos ahora las direcciones en alta resolución y veamos el estado de los diferentes bits de la coordenada Y y de la dirección de videomemoria que le corresponde:
| Coord. F | Coord. Y | Coord. Y (Binario) | Direccion (0,y) (HEX) | (Binario) | Tercio (0-2) | Fila en el tercio |
|---|---|---|---|---|---|---|
| 0 | 0 | 00000000b | $4100 | 0100000000000000b | 0 (00b) | 0 |
| 0 | 1 | 00000001b | $4200 | 0100000100000000b | 0 (00b) | 0 |
| 0 | 2 | 00000010b | $4300 | 0100001000000000b | 0 (00b) | 0 |
| 0 | 3 | 00000011b | $4400 | 0100001100000000b | 0 (00b) | 0 |
| 0 | 4 | 00000100b | $4500 | 0100010000000000b | 0 (00b) | 0 |
| 0 | 5 | 00000101b | $4600 | 0100010100000000b | 0 (00b) | 0 |
| 0 | 6 | 00000110b | $4700 | 0100011000000000b | 0 (00b) | 0 |
| 0 | 7 | 00000111b | $4800 | 0100011100000000b | 0 (00b) | 0 |
| 1 | 8 | 00001000b | $4020 | 0100000000100000b | 0 (00b) | 1 |
| 1 | 9 | 00001001b | $4120 | 0100000100100000b | 0 (00b) | 1 |
| 1 | 10 | 00001010b | $4220 | 0100001000100000b | 0 (00b) | 1 |
| 1 | 11 | 00001011b | $4320 | 0100001100100000b | 0 (00b) | 1 |
| 1 | 12 | 00001100b | $4420 | 0100010000100000b | 0 (00b) | 1 |
| (…) | (…) | (…) | (…) | (…) | (…) | (…) |
Como puede verse, la diferencia entre la composición de baja resolución y la de alta resolución es la modificación de los 3 bits menos significativos de la parte alta de la dirección, que son un reflejo de los 3 bits bajos de la coordenada Y.
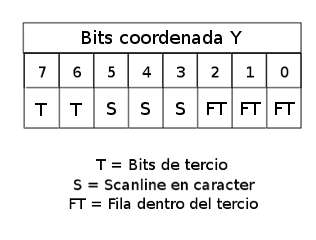
Si examinamos en binario la coordenada Y, vemos que ésta se puede descomponer en 2 bits de Tercio de Pantalla, 3 bits de Fila Dentro del Tercio (FT o N en los ejemplos) y 3 bits de Scanline Dentro Del Carácter (S):
Por otra parte, ya sabemos que C es X / 8, por lo que ya tenemos todos los componentes para realizar nuestra rutina de cálculo de dirección de memoria.
Así pues, la composición final de la dirección de memoria del pixel (x,y) se define de la siguiente forma:
Cálculo de la dirección del pixel (x,y)
No obstante, recordemos que esta dirección de memoria obtenida hace referencia a 8 píxeles, por lo que necesitamos obtener además la información del número de bit con el que se corresponde nuestro pixel, que podemos extraer del resto de la división entre 8 de la coordenada X (P = X and %00000111).
La rutina resultante es similar a la vista en baja resolución con la descomposición de la coordenada Y en el “número de scanline” (0-7) y la “fila dentro del tercio (0-7)”:
;------------------------------------------------------------- ; Get_Pixel_Offset_HR(x,y) ; Obtener la direccion de memoria del pixel (x,y). ; ; Entrada: B = Y, C = X ; Salida: HL = Direccion de memoria del caracter con (x,y) ; A = Posicion del pixel (0-7) en el byte. ;------------------------------------------------------------- Get_Pixel_Offset_HR: ; Calculo de la parte alta de la direccion: ld a, b and %00000111 ; A = 00000SSSb ld h, a ; Lo guardamos en H ld a, b ; Recuperamos de nuevo Y rra rra rra ; Rotamos para asi obtener el tercio and %00011000 ; con un and 00011000b -> 000TT000b or h ; H = H or a = 00000SSSb or 000TT000b or %01000000 ; Mezclamos H con 01000000b (vram) ld h, a ; Establecemos el "H" definitivo ; Calculo de la parte baja de la direccion: ld a, c ; A = coordenada X rra rra rra ; Rotamos para obtener CCCCCb and %00011111 ; A = A and 31 = 000CCCCCb ld l, a ; L = 000CCCCCb ld a, b ; Recuperamos de nuevo Y rla ; Rotamos para obtener NNN rla and %11100000 ; A = A and 11100000b or l ; L = NNNCCCCC ld l, a ; Establecemos el "L" definitivo ; Finalmente, calcular posicion relativa del pixel: ld a, c ; Recuperamos la coordenada X and %00000111 ; and 00000111 para obtener pixel ; A = 00000PPP ret
Esta rutina de 128 t-estados nos devuelve el valor de la dirección calculado en HL y la posición relativa del pixel dentro del byte:
| Valor de A | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| Posición del pixel desde la izquierda | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Posición del pixel dentro del byte (Bit) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Esta posición relativa del pixel nos sirve para 2 cosas:
Por una parte, cuando realicemos rutinas de impresión de sprites con movimiento pixel a pixel, este valor nos puede servir para tratar los sprites (rotarlos) de cara a su impresión en posiciones de byte.
Por otra parte, si necesitamos activar (PLOT, bit=1), desactivar (UNPLOT, b=0) o testear el estado del pixel (x,y), podremos utilizar este valor “posición del pixel” para generar una máscara de pixel.
Si queremos convertir la posición del pixel en una máscara de pixel (por ejemplo, convertir A=6 en el bit 6 activo (A=%01000000), podemos hacerlo con un bucle:
and %00000111 ; and 00000111 para obtener pixel ; A = 00000PPP, y además setear ZF si es 0 ;--- Nuevo código --- ld b, a ; Poner en B el numero de pixel ld a, %10000000 ; Activar sólo el bit 7 de A jr z, getpixoff_norotate ; Si el ''and %00000111' dice que A == 0 ; entonces ya no necesitamos rotar getpixoff_loop: rra ; Rotar A a la derecha B veces djnz getpixoff_lop getpixoff_norotate: ; Ahora A es una máscara de pixel ;--- Fin nuevo código --- ret
Obtención y uso de la Máscara de Pixel
Nuestra rutina de coordenación nos devuelve en HL la dirección de memoria que contiene el pixel (x,y) y en A la posición relativa del pixel dentro de dicha dirección.
Para poder modificar el pixel exacto al que hacen referencia la pareja de datos HL y A resulta necesario convertir A en una “máscara de pixel” que nos permita manipular la memoria con sencillas operaciones lógicas sin afectar al estado de los demás píxeles.
Esta “máscara de pixel” tiene activo el bit 8-pixel ya que el pixel 0 es el pixel de más a la izquierda de los 8, es decir, el bit 7 de la dirección:
| Bit activo | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| Pixel | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
La máscara que debemos generar, en función del valor de A, es:
| Valor de A | Máscara de pixel |
|---|---|
| 0 | 10000000b |
| 1 | 01000000b |
| 2 | 00100000b |
| 3 | 00010000b |
| 4 | 00001000b |
| 5 | 00000100b |
| 6 | 00000010b |
| 7 | 00000001b |
La porción de código que hace esta conversión es la siguiente:
ld b, a ; Cargamos A (posicion de pixel) en B inc b ; Incrementamos B (para pasadas del bucle) xor a ; A = 0 scf ; Set Carry Flag (A=0, CF=1) pix_rotate_bit: rra ; Rotamos A a la derecha B veces djnz pix_rotate_bit
La rutina pone A a cero y establece el Carry Flag a 1, por lo que la primera ejecución de RRA (que siempre se realizará) ubica el 1 del CF en el bit 7 de A. A continuación el DJNZ que se realiza “B” veces mueve ese bit a 1 a la derecha (también “B” veces) dejando A con el valor adecuado según la tabla que acabamos de ver.
En formato de rutina:
;-------------------------------------------------------- : Relative_to_Mask: Convierte una posicion de pixel ; relativa en una mascara de pixel. ; IN: A = Valor relativo del pixel (0,7) ; OUT: A = Pixel Mask (128-1) ; CHANGES: B, F ;-------------------------------------------------------- Relative_to_Mask: ld b, a ; Cargamos A (posicion de pixel) en B inc b ; Incrementamos B (para pasadas del bucle) xor a ; A = 0 scf ; Set Carry Flag (A=0, CF=1) pix_rotate_bit: rra ; Rotamos A a la derecha B veces djnz pix_rotate_bit ret
Mediante esa máscara podemos activar (PLOT), desactivar (UNPLOT) y testear (TEST) el estado del pixel en cuestión:
; Activar el pixel apuntado por HL usando la máscara A Plot_Pixel_HL: or (hl) ld (hl), a ret ; Desactivar el pixel apuntado por HL usando la máscara A Unplot_Pixel_HL: cpl A and (hl) ld (hl), a ret ; Testear el pixel apuntado por HL usando la máscara A Test_Pixel_HL: and (hl) ret
La anterior rutina de PLOT funciona realizando un OR entre la máscara de pixel y el estado de actual de la memoria, y luego escribiendo el resultado de dicho OR en la videoram. De esta forma, sólo alteramos el pixel sobre el que queremos escribir.
Explicándolo con un ejemplo, supongamos que queremos escribir en el pixel (3,0) de la pantalla y ya hay píxeles activos en (0,0) y (7,0):
Pixeles activos en (16384) = 10000001 Máscara de pixel = 00010000
Si ejecutaramos un simple ld (hl), a, el resultado de la operación eliminaría los 2 píxeles activos que ya teníamos en memoria:
Pixeles activos en (16384) = 10000001 Máscara de pixel A = 00010000 OPERACION (HL)=A = ld (hl), a Resultado en (16384) = 00010000
Mediante el OR entre la máscara de pixel y la videomemoria conseguimos alterar el estado de (3,0) sin modificar los píxeles ya existentes:
Pixeles activos en (16384) = 10000001 Máscara de pixel A = 00010000 OPERACION A = A or (hl) = or (hl) Resultado en A = 10010001 OPERACION (HL)=A = ld (hl), a Resultado en (16384) = 10010001
Si en lugar de un OR hubieramos complementado A (cpl A) y hubieramos hecho un AND, habríamos puesto a 0 el bit (y por tanto el pixel):
Pixeles activos en (16384) = 10000001 Máscara de pixel A = 00010000 OPERACION A = cpl(A) = 11101111 OPERACION A = A or (hl) = and (hl) Resultado en A = 10000001 OPERACION (HL)=A = ld (hl), a Resultado en (16384) = 10000001
El cálculo de memoria y la escritura de un pixel quedaría pues de la siguiente forma:
ld c, 127 ; X = 127 ld b, 95 ; Y = 95 call Get_Pixel_Offset_HR ; Calculamos HL y A or (hl) ; OR de A y (HL) ld (hl), a ; Activamos pixel
La primera pregunta que nos planteamos es, si es imprescindible disponer de una máscara de pixel para dibujar o borrar píxeles, ¿por qué no incluir este código de rotación de A directamente en la rutina de coordenación? La respuesta es, “depende de para qué vayamos a utilizar la rutina”.
Si la rutina va a ser utilizada principalmente para trazar píxeles, resultará conveniente incorporar al final de Get_Pixel_Offset_HR() el cálculo de la máscara, y devolver en A dicha máscara en lugar de la posición relativa del pixel.
Pero lo normal en el desarrollo de programas y juegos es que utilicemos la rutina de coordenación para obtener la posición inicial en la que comenzar a trazar sprites, bloques (del mapeado), fuentes de texto, marcadores. En ese caso es absurdo emplear “ciclos de reloj” adicionales para el cálculo de una máscara que sólo se utiliza en el trazado de puntos. En esas circunstancias resulta mucho más útil disponer de la posición relativa del pixel, para, como ya hemos comentado, conocer la cantidad de bits que necesitamos rotar estos datos gráficos antes de su trazado.
Por ese motivo, no hemos agregado esta pequeña porción de código a la rutina de Get_Pixel_Offset, siendo el programador quien debe decidir en qué formato quiere obtener la salida de la rutina.
La rutina de la ROM PIXEL-ADDRESS
Curiosamente, los usuarios de Spectrum tenemos disponible en la memoria ROM una rutina parecida, llamada PIXEL-ADDRESS (o PIXEL-ADD), utilizada por las rutinas POINT y PLOT de la ROM (y de BASIC). La rutina está ubicada en $22aa y su código es el siguiente:
; THE 'PIXEL ADDRESS' SUBROUTINE ; This subroutine is called by the POINT subroutine and by the PLOT ; command routine. Is is entered with the co-ordinates of a pixel in ; the BC register pair and returns with HL holding the address of the ; display file byte which contains that pixel and A pointing to the ; position of the pixel within the byte. ; ; IN: (C,B) = (X,Y) ; OUT: HL = address, A = pixel relative position in (HL) $22aa PIXEL-ADD ld a,$af ; Test that the y co-ordinate (in sub b ; B) is not greater than 175. jp c,24F9,REPORT-B ld b,a ; B now contains 175 minus y. $22b1 PIXEL_ADDRESS_B: ; Entramos aqui para saltarnos la limitacion ; hacia las 2 ultimas lineas de pantalla. and a ; A holds b7b6b5b4b3b2b1b0, rra ; the bite of B. And now ; 0b7b6b5b4b3b2b1. scf rra ; Now 10b7b6b5b4b3b2. and a rra ; Now 010b7b6b5b4b3. xor b and $f8 ; Finally 010b7b6b2b1b0, so that xor b ; H becomes 64 + 8*INT (B/64) + ld h,a ; B (mod 8), the high byte of the ld a,c ; pixel address. C contains X. rlca ; A starts as c7c6c5c4c3c2c1c0. rlca rlca ; And is now c2c1c0c7c6c5c4c3. xor b and $c7 xor b ; Now c2c1b5b4b3c5c4c3. rlca rlca ; Finally b5b4b3c7c6c5c4c3, so ld l,a ; that L becomes 32*INT (B(mod ld a,c ; 64)/8) + INT(x/8), the low byte. and $07 ; A holds x(mod 8): so the pixel ret ; is bit (A - 7) within the byte.
Esta rutina tiene una serie de ventajas: Entrando por $22b1 tenemos 23 instrucciones (107 t-estados) que realizan el cálculo de la dirección de memoria además de la posición del pixel dentro del byte al que apunta dicha dirección. La rutina está ubicada en ROM, por lo que ahorramos esta pequeña porción de espacio en nuestro programa. Además, no usa la pila, no usa registros adicionales a B, C, HL y A, y no altera los valores de B y C durante el cálculo.
Nótese que aunque la rutina está ubicada en $22aa y se entra con los valores (x,y) en C y B, el principio de la rutina está diseñado para evitar que PLOT y POINT puedan acceder a las 2 últimas filas (16 últimos píxeles) de la pantalla. Para saltarnos esta limitación entramos saltando con un call a $22b1 con la coordenada X en el registro C y la coordenada Y en los registros A y B:
ld a, (coord_x) ld c, a ld a, (coord_y) ld b, a call $22b1
De esta forma no sólo nos saltamos la limitación de acceso a las 2 últimas líneas de la pantalla sino que podemos especificar las coordenadas empezando (0,0) en la esquina superior izquierda, con el sistema tradicional de coordenadas, en contraposición al PLOT de BASIC (y de la ROM), donde se comienza a contar la altura como Y = 0 en la parte inferior de la pantalla (empezando en 191-16=175).
Veamos un ejemplo de uso de la rutina de coordenación de la ROM:
; Ejemplo de uso de pixel-address (ROM) ORG 50000 PIXEL_ADDRESS EQU $22b1 entrada: ; Imprimimos un solo pixel en (0,0) ld c, 0 ; X = 0 ld b, 0 ; Y = 0 ld a, b ; A = Y = 0 call PIXEL_ADDRESS ; HL = direccion (0,0) ld a, 128 ; A = 10000000b (1 pixel). ld (hl), a ; Imprimimos el pixel ; Imprimimos 8 pixeles en (255,191) ld c, 255 ; X = 255 ld b, 191 ; Y = 191 ld a, b ; A = Y = 191 call PIXEL_ADDRESS ld a, 255 ; A = 11111111b (8 pixeles) ld (hl), a ; Imprimimos 4 pixeles en el centro de la pantalla ld c, 127 ; X = 127 ld b, 95 ; Y = 95 ld a, b ; A = Y = 95 call PIXEL_ADDRESS ld a, %10101010 ; A = 10101010b (4 pixeles) ld (hl), a loop: ; Bucle para no volver a BASIC y que jr loop ; no se borren la 2 ultimas lineas END 50000
La ejecución del anterior programa nos dejará la siguiente información gráfica en pantalla:
Nótese que la rutina de la ROM nos devuelve en A la posición relativa del pixel cuyas coordenadas hemos proporcionado, por lo que podemos convertir A en una máscara de pixel a la salida de la rutina encapsulando PIXEL-ADDRESS en una rutina “propia” que haga ambas operaciones, a cambio de 2 instrucciones extras (un call y un RET adicionales):
PIXEL_ADDRESS EQU $22b1 ;---------------------------------------------------------- ; Rutina que encapsula a PIXEL_ADDRESS calculando pix-mask. ; IN: (C,B) = (X,Y) ; OUT: HL = address, A = pixel mask ;---------------------------------------------------------- PIXEL_ADDRESS_MASK: call PIXEL_ADDRESS ; Llamamos a la rutina de la ROM ld b, a ; Cargamos A (posicion de pixel) en B inc b ; Incrementamos B (para pasadas del bucle) xor a ; A = 0 scf ; Set Carry Flag (A=0, CF=1) pix_rotate_bit: rra ; Rotamos A a la derecha B veces djnz pix_rotate_bit ret
Cálculo de posiciones de pixeles mediante tabla
Hasta ahora hemos visto cómo calcular la dirección de memoria de un pixel (x,y) mediante descomposición de las coordenadas y composición de la dirección destino utilizando operaciones lógicas y de desplazamiento.
La alternativa a este método es la utilización de una Look Up Table (LUT), una tabla de valores precalculados mediante la cual obtener la dirección destino dada una variable concreta.
En nuestro caso, crearíamos una Lookup Table (LUT) que se indexaría mediante la coordenada Y, de tal modo que la dirección destino de un pixel X,Y sería:
DIRECCION_DESTINO = Tabla_Offsets_Linea[Y] + (X/8) PIXEL_EN_DIRECCION = Resto(X/8) = X AND %00000111
La tabla de offsets de cada inicio de línea tendría 192 elementos de 2 bytes (tamaño de una dirección), por lo que ocuparía en memoria 384 bytes. A cambio de esta “elevada” ocupación en memoria, podemos obtener rutinas más rápidas que las de composición de las coordenadas.
A continuación se muestra la tabla de offsets precalculados:
Scanline_Offsets:
DW 16384, 16640, 16896, 17152, 17408, 17664, 17920, 18176
DW 16416, 16672, 16928, 17184, 17440, 17696, 17952, 18208
DW 16448, 16704, 16960, 17216, 17472, 17728, 17984, 18240
DW 16480, 16736, 16992, 17248, 17504, 17760, 18016, 18272
DW 16512, 16768, 17024, 17280, 17536, 17792, 18048, 18304
DW 16544, 16800, 17056, 17312, 17568, 17824, 18080, 18336
DW 16576, 16832, 17088, 17344, 17600, 17856, 18112, 18368
DW 16608, 16864, 17120, 17376, 17632, 17888, 18144, 18400
DW 18432, 18688, 18944, 19200, 19456, 19712, 19968, 20224
DW 18464, 18720, 18976, 19232, 19488, 19744, 20000, 20256
DW 18496, 18752, 19008, 19264, 19520, 19776, 20032, 20288
DW 18528, 18784, 19040, 19296, 19552, 19808, 20064, 20320
DW 18560, 18816, 19072, 19328, 19584, 19840, 20096, 20352
DW 18592, 18848, 19104, 19360, 19616, 19872, 20128, 20384
DW 18624, 18880, 19136, 19392, 19648, 19904, 20160, 20416
DW 18656, 18912, 19168, 19424, 19680, 19936, 20192, 20448
DW 20480, 20736, 20992, 21248, 21504, 21760, 22016, 22272
DW 20512, 20768, 21024, 21280, 21536, 21792, 22048, 22304
DW 20544, 20800, 21056, 21312, 21568, 21824, 22080, 22336
DW 20576, 20832, 21088, 21344, 21600, 21856, 22112, 22368
DW 20608, 20864, 21120, 21376, 21632, 21888, 22144, 22400
DW 20640, 20896, 21152, 21408, 21664, 21920, 22176, 22432
DW 20672, 20928, 21184, 21440, 21696, 21952, 22208, 22464
DW 20704, 20960, 21216, 21472, 21728, 21984, 22240, 22496
En hexadecimal (para ver la relación entre los aumentos de líneas y el de scanlines y bloques):
Scanline_Offsets:
DW $4000, $4100, $4200, $4300, $4400, $4500, $4600, $4700
DW $4020, $4120, $4220, $4320, $4420, $4520, $4620, $4720
DW $4040, $4140, $4240, $4340, $4440, $4540, $4640, $4740
DW $4060, $4160, $4260, $4360, $4460, $4560, $4660, $4760
DW $4080, $4180, $4280, $4380, $4480, $4580, $4680, $4780
DW $40a0, $41a0, $42a0, $43a0, $44a0, $45a0, $46a0, $47a0
DW $40c0, $41c0, $42c0, $43c0, $44c0, $45c0, $46c0, $47c0
DW $40e0, $41e0, $42e0, $43e0, $44e0, $45e0, $46e0, $47e0
DW $4800, $4900, $4a00, $4b00, $4c00, $4d00, $4e00, $4f00
DW $4820, $4920, $4a20, $4b20, $4c20, $4d20, $4e20, $4f20
DW $4840, $4940, $4a40, $4b40, $4c40, $4d40, $4e40, $4f40
DW $4860, $4960, $4a60, $4b60, $4c60, $4d60, $4e60, $4f60
DW $4880, $4980, $4a80, $4b80, $4c80, $4d80, $4e80, $4f80
DW $48a0, $49a0, $4aa0, $4ba0, $4ca0, $4da0, $4ea0, $4fa0
DW $48c0, $49c0, $4ac0, $4bc0, $4cc0, $4dc0, $4ec0, $4fc0
DW $48e0, $49e0, $4ae0, $4be0, $4ce0, $4de0, $4ee0, $4fe0
DW $5000, $5100, $5200, $5300, $5400, $5500, $5600, $5700
DW $5020, $5120, $5220, $5320, $5420, $5520, $5620, $5720
DW $5040, $5140, $5240, $5340, $5440, $5540, $5640, $5740
DW $5060, $5160, $5260, $5360, $5460, $5560, $5660, $5760
DW $5080, $5180, $5280, $5380, $5480, $5580, $5680, $5780
DW $50a0, $51a0, $52a0, $53a0, $54a0, $55a0, $56a0, $57a0
DW $50c0, $51c0, $52c0, $53c0, $54c0, $55c0, $56c0, $57c0
DW $50e0, $51e0, $52e0, $53e0, $54e0, $55e0, $56e0, $57e0
La tabla ha sido generada mediante el siguiente script en python:
$ cat specrows.py #!/usr/bin/python print "Scanline_Offsets:" for tercio in range(0,3): for caracter in range(0,8): print " DW", for scanline in range(0,8): # Componer direccion como 010TTSSSNNN00000 base = 16384 direccion = base + (tercio * 2048) direccion = direccion + (scanline * 256) direccion = direccion + (caracter * 32) print str(direccion), if scanline!=7: print ",", print
La tabla de valores DW estaría incorporada en nuestro programa y por tanto pasaría a formar parte del “binario final”, incluyendo en este aspecto la necesidad de carga desde cinta.
Si por algún motivo no queremos incluir la tabla en el listado, podemos generarla en el arranque de nuestro programa en alguna posición de memoria libre o designada a tal efecto mediante la siguiente rutina:
;-------------------------------------------------------- ; Generar LookUp Table de scanlines en memoria. ; Rutina por Derek M. Smith (2005). ;-------------------------------------------------------- Scanline_Offsets EQU $f900 Generate_Scanline_Table: ld de, $4000 ld hl, Scanline_Offsets ld b, 192 genscan_loop: ld (hl), e inc l ld (hl), d ; Guardamos en (HL) (tabla) inc hl ; el valor de DE (offset) ; Recorremos los scanlines y bloques en un bucle generando las ; sucesivas direccione en DE para almacenarlas en la tabla. ; Cuando se cambia de caracter, scanline o tercio, se ajusta: inc d ld a, d and %00000111 jr nz, genscan_nextline ld a, e add a, 32 ld e, a jr c, genscan_nextline ld a, d sub 8 ld d, a genscan_nextline: djnz genscan_loop ret
La anterior rutina ubicará en memoria una tabla con el mismo contenido que las ya vistas en formato DW.
Get_Pixel_Offset_LUT
Una vez tenemos generada la tabla (ya sea en memoria o pregenerada en el código de nuestro programa), podemos indexar dicha tabla mediante la coordenada Y y sumar la coordenada X convertida en columna para obtener la dirección de memoria del pixel solicitado, y la posición relativa del mismo en el byte:
;------------------------------------------------------------- ; Get_Pixel_Offset_LUT_HR(x,y): ; ; Entrada: B = Y, C = X ; Salida: HL = Direccion de memoria del pixel (x,y) ; A = Posicion relativa del pixel en el byte ;------------------------------------------------------------- Get_Pixel_Offset_LUT_HR: ld de, Scanline_Offsets ; Direccion de nuestra LUT ld l, b ; L = Y ld h, 0 add hl, hl ; HL = HL * 2 = Y * 2 add hl, de ; HL = (Y*2) + ScanLine_Offset ; Ahora Offset = [HL] ld a, (hl) ; Cogemos el valor bajo de la direccion en A inc l ld h, (hl) ; Cogemos el valor alto de la direccion en H ld l, a ; HL es ahora Direccion(0,Y) ; Ahora sumamos la X, para lo cual calculamos CCCCC ld a, c ; Calculamos columna rra rra rra ; A = A>>3 = ???CCCCCb and %00011111 ; A = 000CCCCB add a, l ; HL = HL + C ld l, a ld a, c ; Recuperamos la coordenada (X) and %00000111 ; A = Posicion relativa del pixel ret ; HL = direccion destino
Veamos un ejemplo de utilización de las anteriores rutinas:
; Ejemplo de uso de LUT ORG 50000 entrada: call Generate_Scanline_Table ld b, 191 loop_draw: push bc ; Preservamos B (por el bucle) ld c, 127 ; X = 127, Y = B call Get_Pixel_Offset_LUT_HR ld a, %10000000 ; 1 pixel en la parte izquierda del byte ld (hl), a ; Imprimimos el pixel pop bc djnz loop_draw loop: ; Bucle para no volver a BASIC y que jr loop ; no se borren la 2 ultimas lineas END 50000
Y su salida en pantalla:
Optimizando la lectura a través de tablas
El coste de ejecución de la rutina Get_Pixel_Offset_LUT_HR es de 117 t-estados, demasiado elevada por culpa de las costosas (en términos temporales) instrucciones de 16 bits, sobre todo teniendo en cuenta que hemos empleado 384 bytes de memoria en nuestra tabla.
Una ingeniosa solución a este problema consiste en dividir la tabla de 192 direcciones de 16 bits en 2 tablas de 192 bytes cada una que almacenen la parte alta de la dirección en la primera de las tablas y la parte baja de la dirección en la segunda, de tal forma que:
H = Tabla_Parte_Alta[Y] L = Tabla_Parte_Baja[Y]
Si realizamos esta división y colocamos en memoria las tablas de forma que estén alineadas en una dirección múltiplo de 256, el mecanismo de acceso a la tabla será mucho más rápido.
La ubicación de las tablas en memoria en una dirección X múltiplo de 256 tendría el siguiente aspecto:
Sea una Direccion_XX divisible por 256: Direccion_XX hasta Direccion_XX+191 -> Partes bajas de las direcciones de pantalla Direccion_XX+256 hasta Direccion_XX+447 -> Partes altas de las direcciones de pantalla.
El paso de una tabla a otra se realizará incrementando o decrementando la parte alta del registro de 16 bits (inc h o dec h), gracias al hecho de que son 2 tablas múltiplos de 256 y consecutivas en memoria.
Veamos primero la rutina para generar la tabla separando las partes altas y bajas y alineando ambas a una dirección múltiplo de 256:
;---------------------------------------------------------- ; Generar LookUp Table de scanlines en memoria en 2 tablas. ; ; En Scanline_Offsets (divisible por 256) ; -> 192 bytes de las partes bajas de la direccion. ; ; En Scanline_Offsets + 256 (divisible por 256) ; -> 192 bytes de las partes altas de la direccion. ; ; Rutina por Derek M. Smith (2005). ;---------------------------------------------------------- Scanline_Offsets EQU 64000 ; Divisible por 256 Generate_Scanline_Table_Aligned: ld de, $4000 ld hl, Scanline_Offsets ld b, 192 genscan_loop: ld (hl), e ; Escribimos parte baja inc h ; Saltamos a tabla de partes altas ld (hl), d ; Escribimos parte alta dec h ; Volvemos a tabla de partes bajas inc l ; Siguiente valor ; Recorremos los scanlines y bloques en un bucle generando las ; sucesivas direccione en DE para almacenarlas en la tabla. ; Cuando se cambia de caracter, scanline o tercio, se ajusta: inc d ld a, d and %00000111 jr nz, genscan_nextline ld a, e add a, 32 ld e, a jr c, genscan_nextline ld a, d sub 8 ld d, a genscan_nextline: djnz genscan_loop ret
En el ejemplo anterior, tendremos entre 64000 y 64191 los 192 valores bajos de la dirección, y entre 64256 y 64447 los 192 valores altos de la dirección. Entre ambas tablas hay un hueco de 256-192=64 bytes sin usar que debemos saltar para poder alinear la segunda tabla en un múltiplo de 256.
Estos 64 bytes no se utilizan en la rutina de generación ni (como veremos a continuación) en la de cálculo, por lo que podemos aprovecharlos para ubicar variables de nuestro programa, tablas temporales, etc, y así no desperdiciarlos.
Si necesitaramos reservar espacio en nuestro programa para después generar la tabla sobre él, podemos hacerlo mediante las directivas de preprocesado del ensamblador ORG (Origen) y DS (Define Space). Las siguientes líneas (ubicadas al final del fichero de código) reservan en nuestro programa un array de 448 bytes de longitud y tamaño cero alineado en una posición múltiplo de 256:
ORG 64000 Scanline_Offsets: DS 448, 0
También podemos incluir las 2 tablas “inline” en nuestro programa, y además sin necesidad de conocer la dirección de memoria en que están (por ejemplo, embedidas dentro del código del programa en la siguiente dirección múltiplo de 256 disponible) aprovechando el soporte de macros del ensamblador PASMO:
; Macro de alineacion para PASMO
align macro value
if $ mod value
ds value - ($ mod value)
endif
endm
align 256
Scanline_Offsets:
LUT_Scanlines_LO:
DB $00, $00, $00, $00, $00, $00, $00, $00, $20, $20, $20, $20
DB $20, $20, $20, $20, $40, $40, $40, $40, $40, $40, $40, $40
DB $60, $60, $60, $60, $60, $60, $60, $60, $80, $80, $80, $80
DB $80, $80, $80, $80, $a0, $a0, $a0, $a0, $a0, $a0, $a0, $a0
DB $c0, $c0, $c0, $c0, $c0, $c0, $c0, $c0, $e0, $e0, $e0, $e0
DB $e0, $e0, $e0, $e0, $00, $00, $00, $00, $00, $00, $00, $00
DB $20, $20, $20, $20, $20, $20, $20, $20, $40, $40, $40, $40
DB $40, $40, $40, $40, $60, $60, $60, $60, $60, $60, $60, $60
DB $80, $80, $80, $80, $80, $80, $80, $80, $a0, $a0, $a0, $a0
DB $a0, $a0, $a0, $a0, $c0, $c0, $c0, $c0, $c0, $c0, $c0, $c0
DB $e0, $e0, $e0, $e0, $e0, $e0, $e0, $e0, $00, $00, $00, $00
DB $00, $00, $00, $00, $20, $20, $20, $20, $20, $20, $20, $20
DB $40, $40, $40, $40, $40, $40, $40, $40, $60, $60, $60, $60
DB $60, $60, $60, $60, $80, $80, $80, $80, $80, $80, $80, $80
DB $a0, $a0, $a0, $a0, $a0, $a0, $a0, $a0, $c0, $c0, $c0, $c0
DB $c0, $c0, $c0, $c0, $e0, $e0, $e0, $e0, $e0, $e0, $e0, $e0
Free_64_Bytes:
DB 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
DB 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
DB 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
DB 0, 0, 0, 0
LUT_Scanlines_HI:
DB $40, $41, $42, $43, $44, $45, $46, $47, $40, $41, $42, $43
DB $44, $45, $46, $47, $40, $41, $42, $43, $44, $45, $46, $47
DB $40, $41, $42, $43, $44, $45, $46, $47, $40, $41, $42, $43
DB $44, $45, $46, $47, $40, $41, $42, $43, $44, $45, $46, $47
DB $40, $41, $42, $43, $44, $45, $46, $47, $40, $41, $42, $43
DB $44, $45, $46, $47, $48, $49, $4a, $4b, $4c, $4d, $4e, $4f
DB $48, $49, $4a, $4b, $4c, $4d, $4e, $4f, $48, $49, $4a, $4b
DB $4c, $4d, $4e, $4f, $48, $49, $4a, $4b, $4c, $4d, $4e, $4f
DB $48, $49, $4a, $4b, $4c, $4d, $4e, $4f, $48, $49, $4a, $4b
DB $4c, $4d, $4e, $4f, $48, $49, $4a, $4b, $4c, $4d, $4e, $4f
DB $48, $49, $4a, $4b, $4c, $4d, $4e, $4f, $50, $51, $52, $53
DB $54, $55, $56, $57, $50, $51, $52, $53, $54, $55, $56, $57
DB $50, $51, $52, $53, $54, $55, $56, $57, $50, $51, $52, $53
DB $54, $55, $56, $57, $50, $51, $52, $53, $54, $55, $56, $57
DB $50, $51, $52, $53, $54, $55, $56, $57, $50, $51, $52, $53
DB $54, $55, $56, $57, $50, $51, $52, $53, $54, $55, $56, $57
Finalmente, veamos si ha merecido la pena el cambio a 2 tablas analizando la nueva rutina de cálculo de dirección:
;------------------------------------------------------------- ; Get_Pixel_Offset_LUT_2(x,y): ; ; Entrada: B = Y, C = X ; Salida: HL = Direccion de memoria del pixel (x,y) ; A = Posicion relativa del pixel en el byte ;------------------------------------------------------------- Get_Pixel_Offset_LUT_2: ld a, c ; Ponemos en A la X rra rra rra ; A = ???CCCCC and %00011111 ; A = 000CCCCCb ld l, b ; B = coordenada Y ld h, Scanline_Offsets/256 ; Parte alta de la dir de tabla add a, (hl) ; A = columna + tabla_baja[linea] inc h ; saltamos a la siguiente tabla ld h, (hl) ; cargamos en H la parte alta ld l, a ; cargamos en L la parte baja ld a, c ; Recuperamos la coordenada (X) and %00000111 ; A = Posicion relativa del pixel ret
El coste de ejecución de esta rutina es de 77 t-estados, incluyendo el RET, la conversión de “X” en “Columna” y la obtención de la posición relativa del pixel.
Cálculos contra Tablas
Como casi siempre en código máquina, nos vemos forzados a elegir entre velocidad y tamaño: las rutinas basadas en tablas son generalmente más rápidas al evitar muchos cálculos, pero a cambio necesitamos ubicar en memoria dichas tablas. Por contra, las rutinas basadas en cálculos ocupan mucho menos tamaño en memoria pero requieren más tiempo de ejecución.
Debemos elegir uno u otro sistema en función de las necesidades y requerimientos de nuestro programa: si disponemos de poca memoria libre y el tiempo de cálculo individual es suficiente, optaremos por la rutina de composición. Si, por contra, la cantidad de memoria libre no es un problema y sí que lo es el tiempo de cálculo, usaremos las rutinas basadas en tablas.
Los programadores debemos muchas veces determinar si una rutina es crítica o no según la cantidad de veces que se ejecute en el “bucle principal” y el porcentaje de tiempo que su ejecución supone en el programa.
Por ejemplo, supongamos una rutina de impresión de sprites de 3×3 bloques: aunque el tiempo de dibujado de los sprites en sí de un juego sea crítico, el posicionado en pantalla para cada sprite sólo se realiza una vez (para su esquina superior izquierda) frente a toda la porción de código que debe imprimir los 9 caracteres (9*8 bytes en pantalla) más sus atributos, con sus correspondientes rotaciones si el movimiento es pixel a pixel. El movimiento entre los diferentes bloques del sprite se realiza normalmente de forma diferencial. Probablemente, invertir “tiempo” para optimizar o “memoria” para tener tablas de precalculo sea más aconsejable en el cuerpo de la rutina de sprites o en tablas de sprites pre-rotados que en la coordenación en sí misma.
La diferencia entre rutinas de tablas y de cálculos se resume en la siguiente tabla:
| Rutina | Tiempo de ejecución | Bytes rutina | Bytes adicionales | Tamaño Total |
|---|---|---|---|---|
| Cálculo | 118 t-estados | 32 | Ninguno | 32 |
| Tablas | 77 t-estados | 17 GetOffset + 32 GenLUT | 448 (384 si aprovechamos los 64 entre tablas) | 443 - 487 bytes |
Cálculo de posiciones de posiciones diferenciales de pixel
Los cálculos de las posiciones de píxeles en alta resolución son “costosos” por lo que a la hora de dibujar sprites, líneas, círculos o cualquier otra primitiva gráfica, lo normal es realizar el cálculo de una posición inicial y moverse diferencialmente respecto a la misma.
Para eso se utilizan rutinas de posicionamiento diferencial como las que ya vimos en los atributos o en baja resolución que nos permitan movernos a cualquiera de los 8 píxeles de alrededor de la dirección HL y posición de pixel que estamos considerando.
Offset del pixel de la izquierda/derecha
En el caso de la coordenación por caracteres (baja resolución), nos bastaba con decrementar o incrementar HL para ir al carácter siguiente o anterior. En este caso, debemos tener en cuenta que cada byte contiene 8 píxeles, por lo que se hace necesaria una máscara de pixel para referenciar a uno u otro bit dentro del byte apuntado por HL.
Teniendo una máscara de pixel en A, las rutinas de cálculo del pixel a la izquierda y a la derecha del pixel actual se basarían en la ROTACIÓN de dicha máscara comprobando las situaciones especiales en las 2 situaciones especiales que se pueden presentar:
- El pixel se encuentra en 10000000b y queremos acceder al pixel de la izquierda.
- El pixel se encuentra en 00000001b y queremos acceder al pixel de la derecha.
En esos casos se podría utilizar el incremento y decremento de la posición de HL:
; HL = Direccion de pantalla base ; A = Mascara de pixeles Pixel_Izquierda_HL_Mask: rlc a ; Rotamos A a la izquierda ret nc ; Si no se activa el carry flag, volvemos dec l ; Si se activa, hemos pasado de 10000000b ret ; a 00000001b y ya podemos alterar HL Pixel_Derecha_HL_Mask: rrc a ; Rotamos A a la derecha ret nc ; Si no se activa el carry flag, volvemos inc l ; Si se activa, hemos pasado de 00000001b ret ; a 10000000b y ya podemos alterar HL
Son apenas 4 instrucciones, lo que resulta en un cálculo significativamente más rápido que volver a llamar a la rutina de coordenación original.
Nótese cómo en lugar de utilizar dec hl o inc hl (6 t-estados), realizamos un dec l o inc l (4 t-estados), ya que dentro de un mismo scanline de pantalla no hay posibilidad de, moviendo a derecha o izquierda, variar el valor del byte alto de la dirección (siempre y cuando no excedamos los límites de la pantalla por la izquierda o por la derecha). De esta forma ahorramos 2 valiosos ciclos de reloj en una operación que suele realizarse en el bucle más interno de las rutinas de impresión de sprites.
Si en lugar de una máscara de pixel tenemos en A la posición relativa (0-7), podemos utilizar el siguiente código:
; HL = Direccion de pantalla base ; A = Posicion relativa del pixel (0=Pixel de la izquierda) Pixel_Derecha_HL_Rel: inc a ; Incrementamos A and %00000111 ; Si A=8 -> A=0 ret nz ; Si no es cero, hemos acabado inc l ; Si se activa, hemos pasado al byte ret ; siguiente -> alterar HL Pixel_Izquierda_HL_Rel: dec a ; Decrementamos A ret p ; Si no hay overflow (A de 0 a 255), fin and %00000111 ; 11111111b -> 00000111b dec l ; Hemos pasado al byte siguiente -> ret ; alteramos HL
Recordemos que ninguna de estas rutinas contempla los líneas izquierdo y derecho de la pantalla.
Offset del pixel del scanline de arriba/abajo
Moverse un scanline arriba o abajo requiere código adicional, como ya vimos en el apartado de coordenadas de caracteres, para detectar tanto los cambios de tercios como los cambios de caracteres.
| Bits = | Dirección VRAM | Bits de Tercio | Bits de scanline | Bits de Carácter-Y | Bits de Columna |
|---|---|---|---|---|---|
| HL = | 010 | TT | SSS | NNN | CCCCC |
Primero debemos detectar si estamos en el último scanline del carácter, ya que avanzar 1 scanline implicaría poner SSS a 000 e incrementar NNN (carácter dentro del tercio). Al incrementar NNN (carácter dentro del tercio) tenemos que verificar también si NNN pasa de 111 a 1000 lo que supone un cambio de tercio:
El código para incrementar HL hacia el siguiente scanline horizontal detectando los saltos de tercio y de carácter sería el siguiente:
; Avanzamos HL 1 scanline: inc h ; Incrementamos HL en 256 (siguiente scanline) ld a, h ; Cargamos H en A and %00000111 ; Si despues del inc h los 3 bits son 0, ; es porque era 111b y ahora 1000b. jr nz, nofix_abajop ; Si no es cero, hemos acabado (solo inc h). ld a, l ; Es cero, hemos pasado del scanline 7 de un ; caracter al 0 del siguiente: ajustar NNN add a, %00100000 ; Ajustamos NNN (caracter dentro de tercio += 1) ld l, a ; Ahora hacemos la comprobacion de salto de tercio jr c, nofix_abajop ; Si esta suma produce acarreo, habria que ajustar ; tercio, pero ya lo hizo el inc h (111b -> 1000b) ld a, h ; Si no produce acarreo, no hay que ajustar sub %00001000 ; tercio, por lo que restamos el bit TT que sumo ld h, a ; el inc h inicial. nofix_abajop: ; HL contiene ahora la direccion del siguiente scanline ; ya sea del mismo caracter o el scanline 0 del siguiente.
Y para retroceder HL en 1 scanline, usando la misma técnica:
ld a, h and %00000111 ; Comprobamos scanline jr z, Anterior_SL_DEC ; Si es cero, hay salto de caracter dec h ; No es cero, basta HL = HL - 256 ret ; Hemos acabado (solo inc h). Anterior_SL_DEC: ; Hay que ir de caracter 000b a 111b dec h ; Decrementamos H ld a, l ; Ajustamos NNN (caracter en tercio -=1) sub %00100000 ; -32 ld l, a ret c ; Si se produjo carry, no hay que ajustar ld a, h ; Se produjo carry, ajustamos el tercio add a, %00001000 ; por el dec h inicial. (+8) ld h, a
Veamos este mismo código en forma de subrutina, aprovechando con RET la posibilidad de evitar los saltos hacia el final de las rutinas:
;------------------------------------------------------------- ; Siguiente_Scanline_HL: ; Obtener la direccion de memoria del siguiente scanline dada ; en HL la direccion del scanline actual, teniendo en cuenta ; saltos de caracter y de tercio. ; ; Entrada: HL = Direccion del scanline actual ; Salida: HL = Direccion del siguiente scanline ;------------------------------------------------------------- Siguiente_Scanline_HL: inc h ld a, h and %00000111 ret nz ld a, l add a, %00100000 ; +32 ld l, a ret c ld a, h sub %00001000 ; -8 ld h, a ret ; Devolvemos en HL el valor ajustado
La rutina para retroceder al scanline superior es de similar factura, con una pequeña reorganización del código para evitar el salto con jr:
;------------------------------------------------------------- ; Anterior_Scanline_HL: ; Obtener la direccion de memoria del anterior scanline dada ; en HL la direccion del scanline actual, teniendo en cuenta ; saltos de caracter y de tercio. ; ; Entrada: HL = Direccion del scanline actual ; Salida: HL = Direccion del anterior scanline ;------------------------------------------------------------- Anterior_Scanline_HL: ld a, h dec h and %00000111 ret nz ld a, %00001000 ; A = 8 add a, h ld h, a ld a, l sub %00100000 ; -32 ld l, a ret nc ld a, h sub %00001000 ; -8 ld h, a ret ; Devolvemos en HL el valor ajustado
La rutina Siguiente_Scanline_HL será especialmente útil en el desarrollo de rutinas de impresión de Sprites, aunque lo normal es que incluyamos el código “inline” dentro de dichas rutinas, para ahorrar los ciclos de reloj usandos en un call+ret.
Otras rutinas
Rutinas cruzadas y de propósito general
En el libro “Lenguaje Máquina Avanzado para ZX Spectrum” de David Webb encontramos 3 rutinas útiles de propósito general para obtener el offset en el área de imagen dada una dirección de atributo o viceversa.
La primera subrutina obtiene la dirección del atributo que corresponde a una dirección de pantalla especificada:
;------------------------------------------------------------- ; Attr_Offset_From_Image (DF-ATT): ; ; Entrada: HL = Direccion de memoria de imagen. ; Salida: DE = Direccion de atributo correspondiente a HL. ;------------------------------------------------------------- Attr_Offset_From_Image: ld a, h rrca rrca rrca and %00000011 or %01011000 ld d, a ld e, l ret
La segunda realiza el proceso inverso: obtiene la dirección del archivo de imagen dada una dirección de atributo. Esta dirección se corresponde con la dirección de los 8 píxeles del primer scanline del carácter.
;------------------------------------------------------------- ; Image_Offset_From_Attr (ATT_DF): ; ; Entrada: HL = Direccion de memoria de atributo. ; Salida: DE = Direccion de imagen correspondiente a HL. ;------------------------------------------------------------- Image_Offset_From_Attr: ld a, h and %00000011 rlca rlca rlca or %01000000 ld d, a ld e, l ret
La tercera es una combinación de localización de offset de imagen, de atributo, y el valor del atributo:
;------------------------------------------------------------- ; Get_Char_Data(c,f) (LOCATE): ; ; Entrada: B = FILA, C = COLUMNA ; Salida: DE = Direccion de atributo. ; HL = Direccion de imagen. ; A = Atributo de (C,F) ;------------------------------------------------------------- Get_Char_Data: ld a, b and %00011000 ld h, a set 6, h rrca rrca rrca or %01011000 ld d, a ld a, b and %00000111 rrca rrca rrca add a, c ld l, a ld e, a ld a, (de) ret
Llamando a la anterior rutina con unas coordenadas (c,f) en C y B obtenemos la dirección de memoria de imagen (HL) y de atributo (DE) de dicho carácter, así como el valor del atributo en sí mismo (A).
Optimizaciones para Get_Pixel_Offset_HR
En ocasiones se puede reescribir una rutina de otra forma para ser ligeramente más eficiente, y las rutinas relacionadas con los gráficos (tanto “dibujar” gráficos como calcular la posición de dibujado) es una firma candidata a optimizarla todo lo posible.
Dean Belfield, en su página L Break Into Program nos proporciona la siguiente rutina optimizada para obtener la dirección de memoria de un pixel dadas su coordenadas (x,y) que requiere 117 t-estados, a costa de no devolvernos la posición relativa del pixel:
; Get screen address - by Dean Belfield ; ; B = Y pixel position ; C = X pixel position ; Returns address in HL Get_Pixel_Address: ld a, b ; Calculate Y2,Y1,Y0 and %00000111 ; Mask out unwanted bits or %01000000 ; Set base address of screen ld h, a ; Store in H ld a, b ; Calculate Y7,Y6 rra ; Shift to position rra rra and %00011000 ; Mask out unwanted bits or h ; OR with Y2,Y1,Y0 ld h, a ; Store in H ld a, b ; Calculate Y5,Y4,Y3 rla ; Shift to position rla and %11100000 ; Mask out unwanted bits ld l, a ; Store in L ld a, c ; Calculate X4,X3,X2,X1,X0 rra ; Shift into position rra rra and %00011111 ; Mask out unwanted bits or l ; OR with Y5,Y4,Y3 ld l, a ; Store in L ret
Finalmente, David Black en su web Overtaken by events nos ofrece la siguiente rutina de 105 t-estados y 26 bytes:
; Get screen address - by David Black ; B = Y pixel position ; C = X pixel position ; Returns address in HL Get_Screen_Address: ld a,b ; Work on the upper byte of the address and %00000111 ; a = Y2 Y1 y0 or %01000000 ; first three bits are always 010 ld h,a ; store in h ld a,b ; get bits Y7, Y6 rra ; move them into place rra rra and %00011000 ; mask off or h ; a = 0 1 0 Y7 Y6 Y2 Y1 Y0 ld h,a ; calculation of h is now complete ld a,b ; get y rla rla and %11100000 ; a = y5 y4 y3 0 0 0 0 0 ld l,a ; store in l ld a,c and %00011111 ; a = X4 X3 X2 X1 or l ; a = Y5 Y4 Y3 X4 X3 X2 X1 ld l,a ; calculation of l is complete ret
Utilizando tablas, en esta misma web podemos ver las siguientes 2 aproximaciones de Patrick Prendergast en base a organizar los datos en memoria alineándolos de una forma que “desperdiciamos” memoria a cambio de que las rutinas sean más rápidas por cómo están alineados esos datos:
; Store the LUT table in the format "y5 y4 y3 y7 y6 y2 y1 y0" ; Lower 5 bits where you need them for y and upper 3 bits to mask ; out to OR with X (which are replaced with 010 anyway). ; This way you'd only need 192 bytes for the table, which could be ; page-aligned for speed. You'd be looking at 69 cycles por request ; and 16 + 192 for the code + table. ; ; By Patrick Prendergast. ; b = y, c = x getScreenAddress: ld h,tbl >> 8 ld l,b ld h,(hl) ld a,%11100000 and h or c ld l,a ld a,%00011111 and h or %01000000 ld h,a ret tbl: ; y5 y4 y3 y7 y6 y2 y1 y0 .db 0,1,2,3,4,5,6,7,32,33... ; Option 2: if you are willing to [potentially] sacrifice ; some space for speed, you can divide the table so that ; you have the low and high bytes of your address list in ; 2 independent tables and have them both page aligned - ; with the low byte first in memory. ; This would completely remove to need to calc y*2 to get ; to your table offset. ; This would require 64 bytes of padding after the 1st table ; (due to both tables being page aligned) meaning you would ; need 448 bytes all up. That being said the 64 bytes of ; padding space is not needed so you can include any other ; data you might need there so it's not wasted. ; Then you would only need 47 cycles to lookup your address! ; ; By Patrick Prendergast. ; b = y, c = x getScreenAddress: ld h,tblLow >> 8 ld l,b ld a,(hl) inc h ld h,(hl) or c ld l,a ret ALIGN 256 tblLow: ; (ADDR & 0xFF) .db 0,0,0,0,0,0,0,0,32,32,32... ALIGN 256 tblHigh: ; (ADDR >> 8) .db 64,65,66,67,68,69,70,71,64,65,66...
Estas rutinas son realmente rápidas, teniendo la segunda un coste de sólo 47 t-estados por cálculo de dirección, a costa de ocupar más espacio por separar la parte alta y la parte baja de la tabla precalculada, y alinearlas en memoria en un múltiplo de 256 para evitar cálculos.
Ficheros
Enlaces
- ZX Display File Organization, por Alvin Albrecht.
- Cálculo de direcciones de pantalla a partir de coordenadas (por Metalbrain).
- Tiempos de ejecución y tamaños de las instrucciones del Z80 (ver z80time.txt).